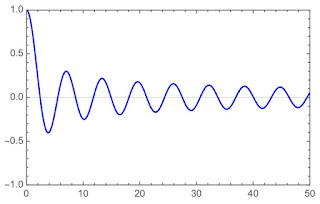
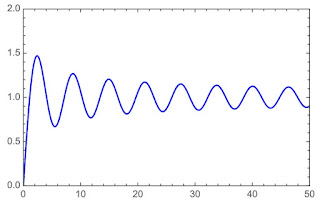
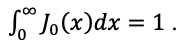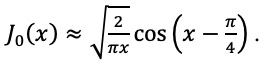John Moulder (1945–2022)

John Moulder,
from Khurana et al. (2008) Med. Phys.,
35:5203, with permission from Wiley.

John Moulder, a leading expert in radiation biology, died about a year ago (on July 17, 2022; I wasn’t aware of his death until last week). When Russ Hobbie and I discuss the possible health risks of weak electric and magnetic fields in Intermediate Physics for Medicine and Biology, we cite a website about powerlines and cancer “that unfortunately no longer exists.” (However, in a previous blog post I found that is does still exist.) We also cite several papers that Moulder wrote with his collaborator Ken Foster about potential electromagnetic field hazards, including

Moulder JE, Foster KR (1995) Biological Effects of Power-Frequency Fields as they Relate to Carcinogenesis. Proceedings of the Society for Experimental Biology and Medicine Volume 209, Pages 309–324.

Moulder JE, Foster KR (1999) Is There a Link Between Exposure to Power-Frequency Electric Fields and Cancer? IEEE Engineering in Medicine and Biology Magazine, Volume 18, Pages 109–116.

Moulder JE, Foster KR, Erdreich LS, McNamee JP (2005) Mobile Phones, Mobile Phone Base Stations and Cancer: A Review. International Journal of Radiation Biology, Volume 81, Pages 189–203.

Foster KR, Moulder JE (2013) Wi-Fi and Health: Review of Current Status and Research. Health Physics, Volume 105, Pages 561–575.

Perhaps my favorite of Moulder’s publications is his Point/Counterpoint article in the journal Medical Physics.

Khurana VG, Moulder JE, Orton CG (2008) There is Currently Enough Evidence and Technology Available to Warrant Taking Immediate Steps to Reduce Exposure of Consumers to Cell-Phone-Related Electromagnetic Radiation. Medical Physics, Volume 35, Pages 5203–5206.

Here is how Moulder is introduced in that paper.

Dr. Moulder obtained his Ph.D. in Biology in 1972 from Yale University. Since 1978, he has served on the faculty of the Medical College of Wisconsin, where he directs the NIH-funded Center for Medical Countermeasures Against Radiological Terrorism. His major research interests include the biological basis for carcinogenesis and cancer therapy, biological aspects of human exposure to non-ionizing radiation, and the prevention and treatment of radiation-induced normal tissue injuries. He has served on a number of national advisory groups concerned with environmental health, non-ionizing radiation, and radiological terrorism; and he currently serves as a radiation biology consultant to NASA.

Are Electromagnetic Fields
Making Me Ill?

In my book Are Electromagnetic Fields Making Me Ill? I wrote:

Radiation biologist John Moulder, of the Medical College of Wisconsin, began maintaining a website titled “Power Lines and Cancer FAQs [frequently asked questions],” which exhaustively summarized the evidence pro and con. Although this website is no longer available online, an archived pdf of it is [13]. In a 1996 article published by IEEE Engineering in Medicine and Biology, Moulder reviewed dozens of studies, and concluded that:

Given the relative weakness of the epidemiology, combined with the extensive and unsupportive laboratory studies, and the biophysical implausibility of interactions at relevant field strengths, it is often difficult to see why there is still any scientific controversy over the issue of power-frequency fields and cancer. [14]

13. large.stanford.edu/publications/crime/references/moulder/moulder.pdf. Access date: January 12, 2022. 

14. Moulder JE (1996) Biological Studies of Power-Frequency Fields and Carcinogenesis. IEEE Engineering in Medicine and Biology Magazine, Volume 15, Pages 31–49.

In a special issue of the International Journal of Radiation Biology dedicated to Moulder, Andrea DiCarlo and her colleagues discussed his work on radiological terrorism.

Through his awarded research grant and cooperative agreements from the NIH and beyond, John leaves behind a legacy of excellent, rigorous, and robust scientific findings, research collaborators who benefited from his expertise and dedication, and a cadre of well-trained students. Although it is impossible to list here all the lives that were touched, and the careers that were impacted by John’s influence, the authors can state with certainty that the field of medical preparedness for a radiation public health emergency would not be where it is now without the steadying hand and role played by Dr. Moulder, both in the early days in the program and during his final years as an active researcher. We are grateful for his years of research and join the entire radiation community in mourning the loss of a great investigator and person.

John Moulder, you were a voice of reason in a crazy world. We’ll miss you.

To hear Moulder in his own words, go to times 4:40 and 5:05 in this video about Power Line Fears.

https://www.youtube.com/watch?v=kf7KWkod3Zw

The Biological Physics Major

Today I want to talk to high school students who, when they attend college, might be majoring in biological physics. What does a biological physics major look like? Below I present my vision of a biological physics curriculum.

Foundational Courses

 Mathematics     

• Calculus 1 
• Calculus 2

Chemistry

• Chemistry 1 
• Chemistry 2 

Biology

• Biology 1 
• Biology 2 

Physics

• Physics 1 
• Physics 2
  

These are the core introductory courses that you absolutely must take. The physics class should be calculus-based. All the science classes need to have a laboratory component (whether as part of the introductory class or as a separate laboratory class to be taken concurrently with the lecture course). In a four-year undergraduate career, these classes represent one course per semester. You’ll probably take most of them in your freshman and sophomore years, because they’ll be prerequisites for more advanced courses. These foundational courses are required for just about any science or engineering major (including premed); if unsure what you want to study you can take them first and then decide your major once you know what you like best. 

Some high school students will have advanced placement credits for many of these classes, which is great, but it’s alright if you don’t. I’ll assume, however, that you’re ready to take calculus the first semester of your freshman year. The best thing you can do in high school to prepare for a biological physics major is to take enough math that you are ready for calculus on day one.

Advanced Courses

Mathematics 

• Multivariable Calculus 
• Differential Equations 

Chemistry 

• Organic Chemistry 
• Biochemistry 

Biology 

• Physiology 

Physics 

• Modern Physics 
• Thermodynamics 
• Electricity and Magnetism
  

Ideally you would take all these advanced courses, but there may be too many for that. Students coming in with advanced placement credits might be able to skip the introductory classes and take these instead. Some universities teach Biochemistry in the chemistry department, and some in the biology department. It doesn’t matter, take one. Many schools offer a two-semester sequence of Organic Chemistry. That would be okay, but it’s probably more Organic than you’ll need. In fact, if pressed for time you might skip Organic altogether, assuming you can still enroll in Biochemistry (which is essential) without needing Organic as a prerequisite. There are many biology classes you could add to this list, but I have included only the one I think is crucial: Physiology. 

If your school is like Oakland University, where I taught, you can take Modern Physics, which is basically a third semester of introductory physics with emphasis on modern topics (relativity, quantum mechanics, nuclear physics). If your school doesn’t have such a course, you could just take the physics department’s Quantum Mechanics class instead. I put E&M on my list because I think it’s the ultimate undergraduate physics course (and my favorite). I’ve noticed that other schools offering biological physics or biophysics curricula sometimes don’t include Electricity and Magnetism. I guess if you can’t cram all these advanced courses into four years and you have to skip something, consider skipping E&M.

Electives

Mathematics

• Linear Algebra 
• Probability and Statistics 

Chemistry

• Physical Chemistry 

Biology

• Genetics 
• Molecular Biology 
• Cell Biology 
• Anatomy 

Physics

• Nuclear Physics 
• Optics 
• Advanced Laboratory
  

I doubt you’ll have time for many of these electives. I believe your undergrad years are a time for getting a liberal education, so I would favor non-science electives over taking all these optional science courses. For example, be sure to take whatever classes are necessary to learn to write well. The Probability and Statistics course is higher priority than Linear Algebra. Don’t bother with Physical Chemistry unless you somehow got through all your physics courses without learning any quantum mechanics. I would load up on the elective biology classes only if you really love biology (you want to study BIOLOGICAL physics, not biological PHYSICS). The most important biology class in the list is, in my opinion, Anatomy. Nuclear Physics is useful if your interests lean toward medical physics; Optics if your interests tend toward biomedical engineering. If you plan on being an experimentalist, an Advanced Laboratory is valuable. 

For you readers who think I’m missing an essential class, or believe some of my recommendations are not needed, add your opinions to the comments section below. I’m sure readers would benefit from other points of view.

Specialty Courses

• Intermediate Physics for Medicine and Biology 1 
• Intermediate Physics for Medicine and Biology 2
  

I may have a vested interest here, but I think a two-semester sequence based on Intermediate Physics for Medicine and Biology should be mandatory. There are some topics in courses like these that are often not covered in other science classes, such as fluid dynamics, diffusion, feedback, and tomography. Not all universities offer such courses. In that case, you might have to take them via independent study, or just do some outside reading. Okay, if you must you can use some other textbook (but you’ll break my heart). 

Any faculty thinking of starting a biological physics major should note that these two specialty courses are the only classes that probably don’t already exist at your institution. The vast majority of the courses I list are already being taught at most colleges and universities.

Capstone Courses

• Colloquium 
• Independent Research
  

If your physics department has a colloquium course take it, at least during your senior year. If not, just attend regularly any research seminars hosted by your physics, chemistry, or biology departments (sometimes these events have free food!). I encourage you to do undergraduate research, even if it means you take fewer advanced courses and electives. My undergraduate research experience was more valuable than any class I ever took.  If your school has few research opportunities, search for a National Science Foundation-supported REU (Research Experience for Undergraduates).

Some students may be attending a college that has no biological physics or biophysics major. In that case, you will just have to adjust this list as best you can to fit your situation. Be flexible. If you have some oddball class that you love, or that is being taught by an outstanding and beloved instructor, don’t hesitate to substitute it for one of the courses on this list. Remember, it’s your education, so do as you want.

I hope this helps you high school students as you plan your college experience. Good luck!

A Short Course in Vector Calculus

Want a short course in vector calculus? You can find one in Intermediate Physics for Medicine and Biology.

Divergence

The divergence is defined in Section 4.1 in IPMB, when discussing the continuity equation. The divergence is one way to differentiate a vector field. I our case, the vector field is the current density (or some other type of flux density), j. Its divergence is defined as 

When you take the divergence of a vector (a quantity that has both magnitude and direction), you get a scalar (a quantity that has magnitude but no direction). In electrostatics, the electrical charge is conserved, implying that the divergence of the electrical current density is zero.

Curl

The curl is defined in Section 8.6, when analyzing electromagnetic induction. It is another way to differentiate a vector,

The symbols x̂, ŷ, and ẑ are unit vectors, and the vertical lines indicate that you follow the rules for determinants when expanding this expression. The curl appears often when analyzing the magnetic field. In our case, the curl of the electric field equations the negative of the time derivative of the magnetic field (Faraday’s law of induction).

Gradient

The gradient is a way to differentiate a scalar field to get a vector. 

 

You can think of the gradient, ∇, as representing the vector x̂ ∂/∂x + ŷ ∂/∂y + ẑ ∂/∂z. The divergence is then found by taking the dot product of the gradient with a vector, and the curl is found by taking the cross product of the gradient with the vector. In electrostatics, V represents of the electric potential (a scalar) and E represents the electric field (a vector). The two are related by

Laplacian

The Laplacian, ∇², is just the dot product of the gradient operator with itself. In other words 

 

You can apply the Laplacian to a vector, but it is more commonly applied to a scalar (such as electrical potential, temperature, or concentration). The Europeans use ∆ to represent the Laplacian, but that’s just weird and we Americans know better than that.

Other Coordinate Systems

We have written the divergence, curl, gradient, and Laplacian in Cartesian coordinates. These operators are more complicated in other coordinate systems. Appendix L of IPMB provides expressions for these operators in cylindrical coordinats of spherical coordinates.

The Divergence Theorem

The divergence theorem says that the volume integral of div J is equal to the surface integral of the normal component of J. We don’t dwell on this theorem in IPMB, but we do ask the reader to derive it in Homework Problem 4 of Chapter 4.

Stokes’ Theorem

We don’t discuss Stokes’ Theorem in IPMB, but I’ve pointed out how we might include a homework problem about it in a previous blog post. Stokes’ theorem says that the line integral of a vector around a closed loop is equal to the surface integral of the curl of that vector of an area bounded by the loop.

div, grad, curl, and all that,
by h. m. schey.

So, almost all the big concepts of vector calculus are presented in IPMB. If, however, you want a little more detail, Russ and I recommend the wonderful book div, grad, curl, and all that, by Harry Schey. I learned vector calculus from the first edition of that book as an undergraduate physics major at the University of Kansas. Schey died five years ago, but his book lives on.

Integral of the Bessel Function

Have you ever been reading a book, making good progress with everything making sense, and then you suddenly stop at say “wait… what?”. That happened to me recently as I was reading Homework Problem 31 in Chapter 12 of Intermediate Physics for Medicine and Biology. (Wait…what? I’m a coauthor of IPMB! How could there be any surprises for me?) The problem is about calculating the two-dimensional Fourier transform of 1/r, and it supplies the following Bessel function identity 

The function J₀ is a Bessel function of the first kind of order zero. What surprised me is that if you let x = kr, you get that the integral of the Bessel function is one,

Really? Here’s a plot of J₀(x).

It oscillates like crazy and the envelope of those oscillations falls off very slowly. In fact, an asymptotic expansion for J₀ at large x is

The leading factor of 1/√x decays so slowly that its integral from zero to infinity does not converge. Yet, when you include the cosine so the function oscillates, the integral does converge. Here’s a plot of

The integral approaches one at large x, but very slowly. So, the expression given in the problem is correct, but I sure wouldn’t want to do any numerical calculations using it, where I had to truncate the endpoint of the integral to something less than infinity. That would be a mess!

Here’s another interesting fact. Bessel functions come in many orders—J₀, J₁, J₂, etc.—and they all integrate to one.

Who’s responsible for these strangely-behaved functions? They’re named after the German astronomer Friedrich Bessel but they were first defined by the Swiss mathematician Daniel Bernoulli (1700–1782), a member of the brilliant Bernoulli family. The Bernoulli equation, mentioned in Chapter 1 of IPMB, is also named for Daniel Bernoulli. 

There was a time when I was in graduate school that I was obsessed with Bessel functions, especially modified Bessel functions that don’t oscillate. I’m not so preoccupied by them now, but they remain my favorite of the many special functions encountered in physics.

Gauss and von Humboldt

The Age of Napoleon,
by Will and Ariel Durant,
Volume 11 of The Story of Civilization.

Regular readers of this blog may recall that over the last few years I’ve been reading Will and Ariel Durant’s magnificent The Story of Civilization. I’m almost done.  I’m currently finishing the final chapters of the last volume: The Age of Napoleon. In the chapter about the German people is a section on science. It states

Two men especially brought scientific honors to Germany in this age—Karl Friedrich Gauss (1777–1855) and Alexander von Humboldt (1769–1859).

Humboldt is never mentioned in Intermediate Physics for Medicine and Biology, but Gauss is everywhere. When speaking of Gauss, the Durants write

We shall not pretend to understand, much less to expound, the discoveries—in number theory, imaginary numbers, quadratic residues, the method of least squares, the infinitesimal calculus—by which Gauss transformed mathematics from what it had been in Newton’s time into an almost new science, which became a tool of the scientific miracles of our time. His observations of the orbit of Ceres (the first planetoid, discovered on January 1, 1801) led him to formulate a new and expeditious method of determining planetary orbits [least squares is discussed in Chapter 11 of IPMB]. He made researches which placed the theory of magnetism and electricity upon a mathematical basis [Gauss’s law for calculating the electric field is discussed in Chapter 6 of IPMB; the now somewhat obsolete unit of magnetic field strength is the gauss]. He was a burden and blessing [definitely a blessing] to all scientists, who believe that nothing is science until it can be stated in mathematical terms. [He also invented the Gaussian probability distribution, which plays a major role in diffusion, discussed in Chapter 4 of IPMB]…. He is now ranked with Archimedes and Newton.

Humboldt was more of a naturalist, and his name never appears in IPMB. But the Durants devoted even more space in their history to him than to Gauss.

The other hero of German Science in this age was Wilhelm von Humboldt’s younger brother Alexander…. In 1796 he began, by accident, the long tour of scientific discovery (rivaling Darwin’s on the Beagle) whose results made him, according to a contemporary quip, “the most famous man in Europe, next to Napoleon.”

Humboldt is particularly famous for his work in geography and geology. I become familiar with him when I taught earth science. I was a new, untenured faculty member at Oakland University when the physics department needed someone to teach our earth science class. OU does not have a geology department, but some students do need a course in earth science, so the physics department was in charge of it. When the faculty member who traditionally taught it retired, I was asked to take it over. I knew nothing about earth science, but neither did anyone else in the department, and being the newest member of the department I didn’t feel that I could say no. I taught the class for about five years, and found that I enjoyed it. Most students in the course were elementary education majors. They weren’t the strongest science students I ever taught, but they were some of the nicest.

Here is what the Durants had to say about Humboldt.

He discovered (1804) that the earth’s magnetic force decreases in intensity from the poles to the equator. He enriched geology with his studies of the igneous origin of certain rocks, the formation of mountains, the geographical distribution of volcanoes. He provided the earliest clues to the laws governing atmospheric disturbances, and thereby shed light on the origin and direction of tropical storms. He made classic studies of air and ocean currents…. His Essai sur la geographie des plantes began the science of biogeography—the study of plant distribution as affected by the physical conditions of the terrain. These and a hundred other contributions, modest in appearance but of wide and lasting influence, were published in thirty volumes from 1805 to 1834 as Voyages de Humboldt et Bonpland aux regions equinoxiales du nouveau continent.

Humboldt is particularly relevant these days as one of the first environmentalists and discoverer of the concept of human-induced climate change. The closest he came to IPMB may be his work on muscle excitation and bioelectricity. In “Alexander von Humboldt and the Concept of Animal Electricity” (Trends in Neurosciences, Volume 20, Pages 239–242, 1997), Helmut Kettenmann wrote

More than two hundred years ago, Alexander von Humboldt helped to establish Galvani's view that muscle and nerve tissue are electrically excitable. His 1797 publication was a landmark for establishing the concept of animal electricity. Almost half a century later, von Humboldt became the mentor of the young du Bois-Reymond. With the help of von Humboldt's promotion, du Bois-Reymond demonstrated convincingly that animal tissue has the intrinsic capacity to generate electrical activity, and thus laid the ground for modern electrophysiology. 

Gauss and Humboldt; what a pair. Put them together with Goethe and Beethoven and Germany around 1800 becomes a pretty interesting place.

Oh, what will I do with myself now that my reading of The Story of Civilization is complete? I guess I will have to focus on the 6th edition of IPMB.

 

My favorite Gauss story, about how as a child he added all the numbers from 1 to 100.

https://www.youtube.com/watch?v=cD9rI4wSc7o

Ken Jennings narrates this video about Alexander von Humboldt.

https://www.youtube.com/watch?v=fj7tRMdmOgs

Alexander von Humboldt and the discovery of climate change.

https://www.youtube.com/watch?v=fYrXE_umWCw

The Partition Function

Any good undergrad statistical mechanics class analyzes the partition function. However, Russ Hobbie and I don’t introduce the partition function in Intermediate Physics for Medicine and Biology. Why not? It’s a long story.

Russ and I do discuss the Boltzmann factor. Suppose you have a system that is in thermal equilibrium with a reservoir at absolute temperature T. Furthermore, suppose your system has discrete energy levels with energy E_i, where i is just an integer labeling the levels. The probability P_i of the system being in level i, is proportional to the Boltzmann factor, exp(–E_i/k_BT),

P_i = C exp(–E_i/k_BT),

where exp is the exponential function, k_B is the Boltzmann constant and C is a constant of proportionality. How do you find C? Any probability must be normalized: the sum of the probabilities must equal one,

Σ P_i = 1 ,

where Σ indicates a summation over all values of i. This means

Σ C exp(–E_i/k_BT) = 1,

or

C = 1/[Σ exp(–E_i/k_BT)] .

The sum in the denominator is the partition function, and is usually given the symbol Z,

Z = Σ exp(–E_i/k_BT) .

In terms of the partition function, the probability of being in state P_i is simply

P_i = (1/Z) exp(–E_i/k_BT) .

An Introduction to Thermal Physics,
by Daniel Schroeder.

Here is what Daniel Schroeder writes in his excellent textbook An Introduction to Thermal Physics,

The quantity Z is called the partition function, and turns out to be far more useful than I would have suspected. It is a “constant” in that it does not depend on any particular state s [he uses “s” rather than “i” to count states], but it does depend on temperature. To interpret it further, suppose once again that the ground state has energy zero. Then the Boltzmann factor for the ground state is 1, and the rest of the Boltzmann factors are less than 1, by a little or a lot, in proportion to the probabilities of the associated states. Thus, the partition function essentially counts how many states are accessible to the system, weighting each one in proportion to its probability.

To see why it’s so useful, let’s define β as 1/k_BT. The Boltzmann factor is then

exp(–βE_i)

and the partition function is

Z = Σ exp(–βE_i) .

The average energy, <E>, is

<E> = [Σ E_i exp(–βE_i)]/[Σ exp(–βE_i)] .

The denominator is just Z. The numerator can be written as the negative of the derivative of Z with respect to β, dZ/dβ (try it and see). So, the average energy is

<E> = – (1/Z) dZ/dβ .

I won’t go on, but there are other quantities that are similarly related to the partition function. It’s surprisingly useful.

Is the partition function hidden in IPMB? You might recognize it in Eq. 3.37, which determines the average kinetic energy of a particle at temperature T (the equipartition of energy theorem) It looks a little different, because there’s a continuous range of energy levels, so the sum is disguised as an integral. You can see it again in Eq. 18.8, when evaluating the average value of the magnetic moment during magnetic resonance imaging. The partition function’s there, but it’s nameless.

Why didn’t Russ and I introduce the partition function? In the Introduction of IPMB Russ wrote: “Each subject is approached in as simple a fashion as possible. I feel that sophisticated mathematics, such as vector analysis or complex exponential notation, often hides physical reality from the student.” Like Russ, I think that the partition function is a trick that makes some equations more compact, but hides the essential physics. So we didn’t use it.

LaTeX and Mathematica

Gene Surdutovich and I are hard at work on the 6th edition of Intermediate Physics for Medicine and Biology. So far, the main thrust of our work involves LaTeX and Mathematica.

Russ Hobbie and I wrote the 5th edition of IPMB using LaTeX, a computer program that is particularly useful for typesetting equations. Russ was our LaTeX guru. I merely read pdf documents that he created and sent him my suggested changes, and then he implemented those changes into the book. With Russ gone, I can no longer escape dealing with LaTeX commands. LaTeX is an extremely powerful piece of software, but mastering it requires a long learning curve. Fortunately, Gene has extensive experience with it.

Let me give you a little peek behind the curtain at typesetting an equation with LaTeX. Equation 4.74 in the 5th edition is the definition of the error function,

In LaTeX it looks like this:

\begin{equation}
\operatorname{erf}(z)=\frac{2}{\sqrt{\uppi}}\int_{0}^{z}e^{-t^{2}}dt.
\label{4.74}%
\end{equation}

Kind of complicated, isn’t it? Sometimes I find myself getting LaTeX and html mixed up. 

LaTeX numbers the equations automatically. They each get a label, such as “\label{4.74}” but this label does not specify the equation number, it’s just a pointer. If I want to refer to this equation later I can write “see Eq.~\ref{4.74}”. If I decide I want to add an equation before Eq. 4.74, I can just give it any label I want—say, “\label{4.73b}”— and then LaTeX will renumber all the equations properly. For a book like IPMB, which has hundreds of equations, this automatic numbering is wonderful.

The index is also created automatically. Whenever I use a term such as “error function” that I want included in the index, I add “\index{Error function}”. LaTeX will keep track of the page number where that code is placed and then include that term with the correct page number in the index. This same sort of internal labeling can be used to create the list of symbols at the end of each chapter,  the list of homework problems, and the section and subsection numbering. In fact, I didn’t have to renumber anything when I added an entire new chapter about... more on that later. LaTeX is amazing. How did I write my PhD dissertation without it?

Also, LaTeX can number and label figures and illustrations, but you have to create the figures using another program. We’ve started using Mathematica for that job. (I’m ashamed to say, I’m not sure what software Russ used.) Mathematica, produced by Wolfram Research, is very powerful, and can do all sorts of symbolic computations. We don’t take advantage of those features, but mainly use the program to make beautiful plots. Fortunately, Gene is even better at Mathematica than at LaTeX, and he helps me a lot. IPMB’s publisher, Springer, says we can use as much color as we want for the 6th edition. Think of the 5th edition of IPMB as like when Dorothy is in Kansas. Publication of the 6th edition will correspond to that memorable scene when she opens the door of the farmhouse and finds herself in the colorful Land of Oz.

Preparing the 6th edition is going to be a long-term project, so don’t expect it anytime soon. Maybe it’ll be ready by the end of 2024, but maybe not. Thanks to all of you who responded to our recent survey. If you have further suggestions, there is still lots of time and we would appreciate hearing any ideas.

And now, back to work!

Dorothy enters the Land of Oz.

https://www.youtube.com/watch?v=F4eQmTizTSo

“If I Only Had a Brain”, from the Wizard of Oz. The song has nothing to do with LaTeX or Mathematica or IPMB, but it’s such a great number that you just have to watch.

https://www.youtube.com/watch?v=nauLgZISozs

Is Quantum Mechanics Necessary for Understanding Magnetic Resonance?

Hanson, L.,
“Is Quantum Mechanics Necessary for
Understanding Magnetic Resonance?”
Concepts Magn.Reson., 32:329–340, 2008

In Chapter 18 of Intermediate Physics for Medicine and Biology, Russ Hobbie and I discuss magnetic resonance imaging. Like many authors, we derive an expression for the magnetization of the tissue using quantum mechanics. Must we use quantum theory? In an article published in Concepts in Magnetic Resonance, Lars Hanson asks the same question: “Is Quantum Mechanics Necessary for Understanding Magnetic Resonance?” (Volume 32, Pages 329–340, 2008). The abstract is given below.

Educational material introducing magnetic resonance typically contains sections on the underlying principles. Unfortunately the explanations given are often unnecessarily complicated or even wrong. Magnetic resonance is often presented as a phenomenon that necessitates a quantum mechanical explanation whereas it really is a classical effect, i.e. a consequence of the common sense expressed in classical mechanics. This insight is not new, but there have been few attempts to challenge common misleading explanations, so authors and educators are inadvertently keeping myths alive. As a result, new students’ first encounters with magnetic resonance are often obscured by explanations that make the subject difficult to understand. Typical problems are addressed and alternative intuitive explanations are provided.

How would IPMB have to be changed to remove quantum mechanics from the analysis of MRI? Quantum ideas first appear in the last paragraph of Section 18.2 about the source of the magnetic moment, where we introduce the idea that the z-component of the nuclear spin in a magnetic field is quantized and can take on values that are integral multiples of the reduced Planck’s constant, ℏ. Delete that paragraph.

Section 18.3 is entirely based on quantum mechanics. To find the average value of the z-component of the spin, we sum over all quantum states, weighted by the Boltzmann factor. The end result is an expression for the magnetization as a function of the magnetic field. We could, alternatively, do this calculation classically. Below is a revised Section 18.3 that uses only classical mechanics and classical thermodynamics.

18.3 The Magnetization

The MR [magnetic resonance] image depends on the magnetization of the tissue. The magnetization of a sample, M, is the average magnetic moment per unit volume. In the absence of an external magnetic field to align the nuclear spins, the magnetization is zero. As an external magnetic field B is applied, the spins tend to align in spite of their thermal motion, and the magnetization increases, proportional at first to the external field. If the external field is strong enough, all of the nuclear magnetic moments are aligned, and the magnetization reaches its saturation value.

We can calculate how the magnetization depends on B. Consider a collection of spins of a nuclear species in an external magnetic field. This might be the hydrogen nuclei (protons) in a sample. The spins do not interact with each other but are in thermal equilibrium with the surroundings, which are at temperature T. We do not consider the mechanism by which they reach thermal equilibrium. Since the magnetization is the average magnetic moment per unit volume, it is the number of spins per unit volume, N, times the average magnetic moment of each spin: M=N<μ>, where μ is the magnetic moment of a single spin.

To obtain the average value of the z component of the magnetic moment, we must average over all spin directions, weighted by the probability that the z component of the magnetic moment is in that direction. Since the spins are in thermal equilibrium with the surroundings, the probability is proportional to the Boltzmann factor of Chap. 3, e^–(U/k_BT) = e^{μBcosθ/k_BT}, where k_B is the Boltzmann constant. The denominator in Eq. 18.8 normalizes the probability:

The factor of sinθ arises when calculating the solid angle in spherical coordinates (see Appendix L). At room temperature μB/(k_BT) ≪ 1 (see Problem 4), and it is possible to make the approximation e^x ≈ 1 + x. The integral in the numerator then has two terms:

The first integral vanishes. The second is equal to 2/3 (hint: use the substitution u = cosθ). The denominator is

The first integral is 2; the second vanishes. Therefore we obtain

The z component of M is

which is proportional to the applied field.

The last place quantum mechanics is mentioned is in Section 18.6 about relaxation times. The second paragraph, starting “One way to analyze the effect…”, can be deleted with little loss of meaning; it is almost an aside.

So, to summarize, if you want to modify Chapter 18 of IPMB to eliminate any reference to quantum mechanics, then 1) delete the last paragraph of Section 18.2, 2) replace Section 18.3 with the modified text given above, and 3) delete the second paragraph in Section 18.6. Then, no quantum mechanics appears, and Planck’s constant is absent. Everything is classical, just the way I like it.

Calculus Made Easy

Intermediate Physics for Medicine and Biology assumes the reader knows calculus. Most medical doctors and biologists have studied some calculus, but I’m not sure they remember much of it. And most high school students, and even college freshman, have yet to take their first calculus course. What should these readers of IPMB do if they don’t know any calculus?  

Calculus Made Easy,
by Silvanus Thompson.

What these readers need is a quick and easy way to learn calculus without delving into all the subtle and complicated details. How can they do that? Read the delightful old book Calculus Made Easy, by Silvanus Thompson. Here’s the prologue:

Considering how many fools can calculate, it is surprising that it should be thought either a difficult or a tedious task for any other fool to learn how to master the same tricks. 

Some calculus-tricks are quite easy. Some are enormously difficult. The fools who write the textbooks of advanced mathematics — and they are mostly clever fools — seldom take the trouble to show you how easy the easy calculations are. On the contrary, they seem to desire to impress you with their tremendous cleverness by going about it in the most difficult way. 

Being myself a remarkably stupid fellow, I have had to unteach myself the difficulties, and now beg to present to my fellow fools the parts that are not hard. Master these thoroughly, and the rest will follow. What one fool can do, another can.

I know what you’re thinking: “That sounds like just what I need, but how much is it going to cost me?” The good news is that you can access the book for free online, at http://calculusmadeeasy.org.

Silvanus P. Thompson

The author, Silvanus Phillips Thompson (1851–1916), was an English physicist and a fellow of the Royal Society. I have a particular fondness for physicists from the Victorian era, especially one such as Thompson who was interested in science education and whose strength was his ability to explain difficult concepts clearly.

For those of you turned off by the dated style of Calculus Made Easy, written in 1910, I suggest Quick Calculus or Used Math instead. For those who, like me, love the Victorian style, I recommend Flatland by Edwin Abbott.

Enjoy!

Calculus Made Easy, by Silvanus P. Thompson, Part 1/2. A LibriVox audiobook. 

https://www.youtube.com/watch?v=hF2FLi5UnlE

 

Calculus Made Easy, by Silvanus P. Thompson, Part 2/2. A LibriVox audiobook.

https://www.youtube.com/watch?v=uqQtQNTKo-A

Terminal Speed of Microorganisms

A Paramecium aurelia seen through an optical microscope.
Source: Wikipedia (http://en.wikipedia.org/wiki/Image:Paramecium.jpg)

Homework Problem 28 at the end of Chapter 2 in Intermediate Physics for Medicine and Biology asks the reader to calculate the terminal speed of an animal falling in air. Although this problem provides insight, it includes a questionable assumption. Russ and I tell the student to “assume that the frictional force is proportional to the surface area of the animal.” If, however, the animal falls at low Reynolds number, this assumption is not valid. Instead, the drag force is given by Stokes’ law, which is proportional to the radius, not the surface area (radius squared). The new homework problem given below asks the reader to calculate the terminal speed for a microorganism falling through water at low Reynolds number.

Section 2.8

Problem 28 ½. Calculate the terminal speed, V, of a paramecium sinking in water. Assume that the organism is spherical with radius R, and that the Reynolds number is small so that the drag force is given by Stokes’ law. Include the effect of buoyancy. Let the paramecium’s radius be 100 microns and its specific gravity be 1.05. Verify that its Reynolds number is small.

The reader will first need to get the density ρ and viscosity η of water, which are ρ = 1000 kg/m³ and η = 0.001 kg/(m s). The specific gravity is not defined in IPMB, but it’s the density divided by the density of water, implying that the density of the paramecium is 1050 kg/m³. Finally, Stokes’ law is given in IPMB as Eq. 4.17, F_drag = –6πRηV.

I’ll let you do your own calculation. I calculate the terminal speed to be about 1 mm/s, so it takes about a fifth of a second to sink one body diameter. The Reynolds number is 0.1, which is small, but not exceptionally small.

You should find that the terminal speed increases as the radius squared, in contrast to a drag force proportional to the surface area for which the terminal speed increases in proportion to the radius. Bigger organisms sink faster. The dependence of terminal speed on size is even more dramatic for aquatic microorganisms than for mammals falling in air. To paraphrase Haldane’s quip, “a bacterium is killed, a diatom is broken, a paramecium splashes,” except the speeds are small enough that none of the “wee little beasties” are really killed (the terminal speed is not terminal...get it?) and splashing is a high Reynolds number phenomenon.

Buoyancy is not negligible for aquatic animals. The effective density of a paramecium in air would be about 1000 kg/m³, but in water its effective density drops to a mere 50 kg/m³. Microorganisms are made mostly of water, so they are almost neutrally buoyant. In this homework problem, the effect of gravity is reduced to only five percent of what it would be if buoyancy were ignored.

A paramecium is a good enough swimmer that it can swim upward against gravity if it wants to. Its surface is covered with cilia that beat together like a Roman galley to produce the swimming motion (ramming speed!).

Whenever discussing terminal speed, one should remember that we assume the fluid is initially at rest. In fact, almost any volume of water will have currents moving at speeds greater than 1 mm/s, caused by tides, gravity, thermal convection, wind driven waves, or the wake of a fish swimming by. A paramecium would drift along with these currents. To observe the motion described in this new homework problem, one must be careful to avoid any bulk movement of water.

If you watched a paramecium sink in still water, would you notice any Brownian motion? You can calculate the root-mean-squared thermal speed with Eq. 4.12 in IPMB, using the mass of the paramecium as four micrograms and a temperature of 20° C. You get approximately 0.002 mm/s. That is less than 1% of the terminal speed, so you wouldn’t notice any random Brownian motion unless you measured extraordinarily carefully.