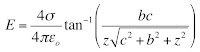In the January 9 post of this blog, I challenged readers to find the electrical potential V(z) that will give you the electric field E(z) of Eq. 6.10 in the 5th edition of Intermediate Physics for Medicine and Biology
In other words, the goal is to find V(z) such that E = − dV/dz produces Eq. 6.10. In the comments at the bottom of the post, a genius named Adam Taylor made a suggestion for V(z) (I love it when people leave comments in this blog). When I tried his expression for the potential, it almost worked, but not quite (of course, there is always a chance I have made a mistake, so check it yourself). But I was able to fix it up with a slight modification. I now present to you, dear reader, the potential:
How do you interpret this ugly beast? The key is the last term, z times the inverse tangent. When you take the z derivative of V(z), you must use the product rule on this term. One derivative in the product rule eliminates the leading z and gives you exactly the inverse tangent you need in the expression for the electric field. The other gives z times a derivative of the inverse tangent, which is complicated. The two terms containing the logarithms are needed to cancel the mess that arises from differentiating tan−1.
I don’t know what there is to gain from having this expression for the potential, but somehow it comforts me to know that if there is an analytic equation for E there is also an analytic equation for V.
Friday, June 26, 2015
Friday, June 19, 2015
Dr. Euler’s Fabulous Formula Cures Many Mathematical Ills
 |
| Dr. Euler's Fabulous Formula, by Paul Nahin. |
eiθ = cosθ + i sinθ .
I liked the book, in part because Nahin and I seem to have similar tastes: we both favor the illustrations of Norman Rockwell over the paintings of Jackson Pollock, we both like to quote Winston Churchill, and we both love limericks:
I used to think math was no fun,Nahin’s book contains a lot of math, and I admit I didn’t go through it all in detail. A large chunk of the text talks about the Fourier series, which Russ Hobbie and I develop in Chapter 11 of IPMB. Nahin motivates the study of the Fourier series as a tool to solve the wave equation. We discuss the wave equation in Chapter 13 of IPMB, but never make the connection between the Fourier series and this equation, perhaps because biomedical applications don’t rely on such an analysis as heavily as, say, predicting how a plucked string vibrates.
‘Cause I couldn’t see how it was done.
Now Euler’s my hero
For I now see why zero,
Equals eπi + 1.
Nahin delights in showing how interesting mathematical relationships arise from Fourier analysis. I will provide one example, closely related to a calculation in IPMB. In Section 11.5, we show that the Fourier series of the square wave (y(t) = 1 for t from 0 to T/2 and equal to -1 for t from T/2 to T) is
y(t) = Σ bk cos(k2πt/T)
where the sum is over all odd values of k (k = 1, 3, 5, ....) and bk = 4/(π k). Evaluate both expressions for y(t) at t = T/4. You get
π/4 = 1 – 1/3 + 1/5 – 1/7 +…
This lovely result is hidden in IPMB’s Eq. 11.36. Warning: this is not a particularly useful algorithm for calculating π, as it converges slowly; including ten terms in the sum gives π = 3.04, which is still over 3% off.
In Figure 11.17, Russ and I discuss the Gibbs phenomenon: spikes that occur in y(t) at discontinuities when the Fourier series includes only a finite number of terms. Nahin makes the same point with the periodic function y(t) = (π – t)/2 for t from 0 to 2π. He describes the history of the Gibbs phenomena, which arises from a series of published letters between Josiah Gibbs, Albert Michelson, A. E. H. Love, and Henri Poincare. Interestingly, the Gibbs phenomenon was discovered long before Gibbs by the English mathematician Henry Wilbraham.
Fourier series did not originate with Joseph Fourier. Euler, for example, was known to write such trigonometric series. Fourier transforms (the extension of Fourier series to nonperiodic functions), on the other hand, were first presented by Fourier. Nahin discusses many of the same topics that Russ and I cover, including the Dirac delta function, Parseval’s theorem, convolutions, and the autocorrelation.
Nahin concludes with a section about Euler the man and mathematical physicist. I found an interesting connection to biology and medicine: when hired in 1727 by the Imperial Russian Academy of Sciences, it was as a professor of physiology. Euler spent several months before he left for Russia studying physiology, so he would not be totally ignorant of the subject when he arrived in Saint Petersburg!
I will end with a funny story of my own. I was working at Vanderbilt University just as Nashville was enticing a professional football team to move there. One franchise that was looking to move was the Houston Oilers. Once the deal was done, folks in Nashville began debating what to call their new team. They wanted a name that would respect the team’s history, but would also be fitting for its new home. Nashville has always prided itself as the home of many colleges and universities, so a name out of academia seemed appropriate. Some professors in Vanderbilt’s Department of Mathematics came up with what I thought was the perfect choice: call the team the Nashville Eulers. Alas, the name didn’t catch on, but at least I never again was uncertain about how to pronounce Euler.
Friday, June 12, 2015
Circularly Polarized Excitation Pulses, Spin Lock, and T1ρ
In Chapter 18 of the 5th edition of Intermediate Physics for Medicine and Biology, Russ Hobbie and I discuss magnetic resonance imaging. We describe how spins precess in a magnetic field, Bo = Bo k, at their Larmor frequency ω, and show that this behavior is particularly simple when expressed in a rotating frame of reference. We then examine radio-frequency excitation pulses by adding an oscillating magnetic field. Again, the analysis is simpler in the rotating frame. In our book, we apply the oscillating field in the laboratory frame’s x-direction, B1 = B1 cos(ωt) i. The equations of the magnetization are complicated in the rotating frame (Eqs. 18.22-18.24), but become simpler when we average over time (Eq. 18.25). The time-averaged magnetization rotates about the rotating frame’s x' axis with angular frequency γB1/2, where γ is the spin’s gyromagnetic ratio. This motion is crucial for exciting the spins; it rotates them from their equilibrium position parallel to the static magnetic field Bo into a plane perpendicular to Bo.
When I teach medical physics (PHY 326 here at Oakland University), I go over this derivation in class, but the students still need practice. I have them analyze some related examples as homework. For instance, the oscillating magnetic field can be in the y direction, B1 = B1 cos(ωt) j, or can be shifted in time, B1 = B1 sin(ωt) i. Sometimes I even ask them to analyze what happens when the oscillating magnetic field is in the z direction, B1 = B1 cos(ωt) k, parallel to the static field. This orientation is useless for exciting spins, but is useful as practice.
Yet another way to excite spins is using a circularly polarized magnetic field, B1 = B1 cos(ωt) i – B1 sin(ωt) j. The analysis of this case is similar to the one in IPMB, with one twist: you don’t need to average over time! Below is a new homework problem illustrating this.
Now let’s assume that an RF excitation pulse rotates the magnetization so it aligns with the x' rotating axis. Once the pulse ends, what happens? Well, nothing happens unless we account for relaxation. Without relaxation the magnetization precesses around the static field, which means it just sits there stationary in the rotating frame. But we know that relaxation occurs. Consider the mechanism of dephasing, which underlies the T2* relaxation time constant. Slight heterogeneities in Bo mean that different spins precess at different Larmor frequencies, causing the spins to lose phase coherence, decreasing the net magnetization.
Next, consider the case of spin lock. Imagine an RF pulse rotates the magnetization so it is parallel to the x' rotating axis. Then, when the excitation pulse is over, immediately apply a circularly polarized RF pulse at the Larmor frequency, called B2, which is aligned along the x' rotating axis. In the rotating frame the magnetization is parallel to B2, so nothing happens. Why bother? Consider those slight heterogeneities in Bo that led to T2* relaxation. They will cause the spins to dephase, picking up a component in the y' direction. But a component along y' will start to precess around B2. Rather than dephasing, B2 causes the spins to wobble around in the rotating frame, precessing about x', with no net tendency to dephase. You just killed the mechanism leading to T2*! Wow!
Will the spins just precess about B2 forever? No, eventually other mechanisms will cause them to relax toward their equilibrium value. Their time constant will not be T1 or T2 or even T2*, but something else called T1ρ. Typcially, T1ρ is much longer than T2*. To measure T1ρ, apply a 90 degree excitation pulse, then apply a RF spin lock oscillation and record the free induction decay. Fit the decay to an exponential, and the time constant you obtain is T1ρ. (I am not a MRI expert: I am not sure how you can measure a free induction decay when a spin lock field is present. I would think the spin lock field would swamp the FID.)
T1ρ is sometimes measured to learn about the structure of cartilage. It is analogous to T1 relaxation in the laboratory frame, which explains its name. Because B2 is typically much weaker than Bo, T1ρ is sensitive to a different range of correlation times than T1 or T2 (see Fig. 18.12 in IPMB).
When I teach medical physics (PHY 326 here at Oakland University), I go over this derivation in class, but the students still need practice. I have them analyze some related examples as homework. For instance, the oscillating magnetic field can be in the y direction, B1 = B1 cos(ωt) j, or can be shifted in time, B1 = B1 sin(ωt) i. Sometimes I even ask them to analyze what happens when the oscillating magnetic field is in the z direction, B1 = B1 cos(ωt) k, parallel to the static field. This orientation is useless for exciting spins, but is useful as practice.
Yet another way to excite spins is using a circularly polarized magnetic field, B1 = B1 cos(ωt) i – B1 sin(ωt) j. The analysis of this case is similar to the one in IPMB, with one twist: you don’t need to average over time! Below is a new homework problem illustrating this.
Problem 13 1/2. Assume you have a static magnetic field in the z direction and an oscillating, circularly polarized magnetic field in the x-y plane, B =Bo k + B1 cos(ωt) i – B1 sin(ωt) j.
a) Use Eq. 18.12 to derive the equations for the magnetization M in the laboratory frame of reference (ignore relaxation).
b) Use Eq. 18.18 to transform to the rotating coordinate system and derive equations for M'.
c) Interpret these results physically.I get the same equations as derived in IPMB (Eq. 18.25) except for a factor of one half; the angular frequency in the rotating frame is ω1 = γ B1. Not having to average over time makes the result easier to visualize. You don’t get a complex motion that—on average—rotates the magnetization. Instead, you get a plain old rotation. You can understand this behavior qualitatively without any math by realizing that in the rotating coordinate system the RF circularly polarized magnetic field is stationary, pointing in the x’ direction. The spins simply precess around the seemingly static B1'= B1 i', just like the spins precess around the static Bo = Bo k in the laboratory frame.
Now let’s assume that an RF excitation pulse rotates the magnetization so it aligns with the x' rotating axis. Once the pulse ends, what happens? Well, nothing happens unless we account for relaxation. Without relaxation the magnetization precesses around the static field, which means it just sits there stationary in the rotating frame. But we know that relaxation occurs. Consider the mechanism of dephasing, which underlies the T2* relaxation time constant. Slight heterogeneities in Bo mean that different spins precess at different Larmor frequencies, causing the spins to lose phase coherence, decreasing the net magnetization.
Next, consider the case of spin lock. Imagine an RF pulse rotates the magnetization so it is parallel to the x' rotating axis. Then, when the excitation pulse is over, immediately apply a circularly polarized RF pulse at the Larmor frequency, called B2, which is aligned along the x' rotating axis. In the rotating frame the magnetization is parallel to B2, so nothing happens. Why bother? Consider those slight heterogeneities in Bo that led to T2* relaxation. They will cause the spins to dephase, picking up a component in the y' direction. But a component along y' will start to precess around B2. Rather than dephasing, B2 causes the spins to wobble around in the rotating frame, precessing about x', with no net tendency to dephase. You just killed the mechanism leading to T2*! Wow!
Will the spins just precess about B2 forever? No, eventually other mechanisms will cause them to relax toward their equilibrium value. Their time constant will not be T1 or T2 or even T2*, but something else called T1ρ. Typcially, T1ρ is much longer than T2*. To measure T1ρ, apply a 90 degree excitation pulse, then apply a RF spin lock oscillation and record the free induction decay. Fit the decay to an exponential, and the time constant you obtain is T1ρ. (I am not a MRI expert: I am not sure how you can measure a free induction decay when a spin lock field is present. I would think the spin lock field would swamp the FID.)
T1ρ is sometimes measured to learn about the structure of cartilage. It is analogous to T1 relaxation in the laboratory frame, which explains its name. Because B2 is typically much weaker than Bo, T1ρ is sensitive to a different range of correlation times than T1 or T2 (see Fig. 18.12 in IPMB).
Friday, June 5, 2015
Robert Plonsey (1924-2015)
 |
| Bioelectricity: A Quantitative Approach, by Plonsey and Barr. |
Plonsey had an enormous impact on my research when I was in graduate school. For example, in 1968 John Clark and Plonsey calculated the intracellular and extracellular potentials produced by a propagating action potential along a nerve axon (“The Extracellular Potential Field of a Single Active Nerve Fiber in a Volume Conductor,” Biophysical Journal, Volume 8, Pages 842−864). Russ and I outline this calculation--which uses Bessel functions and Fourier transforms--in IPMB’s Homework Problem 30 of Chapter 6. In one of my first papers, Jim Woosley, my PhD advisor John Wikswo, and I extended Clark and Plonsey’s calculation to predict the axon’s magnetic field (Woosley, Roth, and Wikswo, 1985, “The Magnetic Field of a Single Axon: A Volume Conductor Model,” Mathematical Bioscience, Volume 76, Pages 1−36). I have described Clark and Plonsey’s groundbreaking work before in this blog.
I associate Plonsey most closely with the development of the bidomain model of cardiac tissue. The 1980s was an exciting time to be doing cardiac electrophysiology, and Duke University, where Plonsey worked, was the hub of this activity. Wikswo, Nestor Sepulveda, and I, all at Vanderbilt University, had to run fast to compete with the Duke juggernaut that included Plonsey, Barr, Ray Ideker, Theo Pilkington, and Madison Spach, as well as a triumvirate of then up-and-coming researchers from my generation: Natalia Trayanova, Wanda Krassowska, and Craig Henriquez. To get a glimpse of these times (to me, the “good old days”), read Henriquez’s “A Brief History of Tissue Models for Cardiac Electrophysiology” (IEEE Transaction on Biomedical Engineering, Volume 61, Pages 1457−1465) published last year.
My first work on the bidomain model was to extend Clark and Plonsey’s calculation of the potential along a nerve axon to an analogous calculation along a cylindrical strand of cardiac tissue, such as a papillary muscle (Roth and Wikswo, 1986, “A Bidomain Model for Extracellular Potential and Magnetic Field of Cardiac Tissue,” IEEE Transaction on Biomedical Engineering, Volume 33, Pages 467−469). I remember what an honor it was for me when Plonsey and Barr cited our paper (and mentioned John and me by name!) in their 1987 article “Interstitial Potentials and Their Change with Depth into Cardiac Tissue” (Biophysical Journal, Volume 51, Pages 547−555). That was heady stuff for a nobody graduate student who could count his citations on his ten fingers.
One day Wikswo returned from a conference and told us about a talk he heard, by either Plonsey or Barr (I don’t recall which), describing the action current distribution produced by a outwardly propagating wave front in a sheet of cardiac tissue (Plonsey and Barr, 1984, “Current Flow Patterns in Two-Dimensional Anisotropic Bisyncytia with Normal and Extreme Conductivities,” Biophysical Journal, Volume 45, Pages 557−571). Wikswo realized immediately that their calculations implied the wave front would have a distinctive magnetic signature, which he and Nestor Sepulveda reported in 1987 (“Electric and Magnetic Fields From Two-Dimensional Anisotropic Bisyncytia,” Biophysical Journal, Volume 51, Pages 557−568).
In another paper, Barr and Plonsey derived a numerical method to solve the bidomain equations including the nonlinear ion channel kinetics (Barr and Plonsey, 1984, “Propagation of Excitation in Idealized Anisotropic Two-Dimensional Tissue,” Biophysical Journal, Volume 45, Pages 1191−1202). This paper was the inspiration for my own numerical algorithm (Roth, 1991, “Action Potential Propagation in a Thick Strand of Cardiac Muscle,” Circulation Research, Volume 68, Pages 162−173). In my paper, I cited several of Plonsey’s articles, including one by Plonsey, Henriquez, and Trayanova about an “Extracellular (Volume Conductor) Effect on Adjoining Cardiac Muscle Electrophysiology” (1988, Medical and Biological Engineering and Computing, Volume 26, Pages 126−129), which shared the conclusion I reached that an adjacent bath can dramatically affect action potential propagation in cardiac tissue. Indeed, Henriquez (Plonsey’s graduate student) and Plonsey were following a similar line of research, resulting in two papers partially anticipating mine (Henriquez and Plonsey, 1990, “Simulation of Propagation Along a Cylindrical Bundle of Cardiac Tissue—I: Mathematical Formulation,” IEEE Transactions on Biomedical Engineering, Volume 37, Pages 850−860; and Henriquez and Plonsey, 1990, “Simulation of Propagation Along a Cylindrical Bundle of Cardiac Tissue—II: Results of Simulation,” IEEE Transactions on Biomedical Engineering, Volume 37, Pages 861−875.)
In parallel with this research, Ideker was analyzing how defibrillation shocks affected cardiac tissue, and in 1986 Plonsey and Barr published two papers presenting their saw tooth model (“Effect of Microscopic and Macroscopic Discontinuities on the Response of Cardiac Tissue to Defibrillating (Stimulating) Currents,” Medical and Biological Engineering and Computing, Volume 24, Pages 130−136; “Inclusion of Junction Elements in a Linear Cardiac Model Through Secondary Sources: Application to Defibrillation,” Volume 24, Pages 127−144). (It’s interesting how many of Plonsey’s papers were published as pairs.) I suspect that if in 1989 Sepulveda, Wikswo and I had not published our article about unipolar stimulation of cardiac tissue (“Current Injection into a Two-Dimensional Anisotropic Bidomain,” Biophysical Journal, Volume 55, Pages 987−999), one of the Duke researchers—perhaps Plonsey himself—would have soon performed the calculation. (To learn more about the Sepulveda et al paper, read my May 2009 blog entry.)
In January 1991 I visited Duke and gave a talk in the Emerging Cardiovascular Technologies Seminar Series, where I had the good fortune to meet with Plonsey. Somewhere I have a videotape of that talk; I suppose I should get it converted to a digital format. When I was working at the National Institutes of Health in the mid 1990s, Plonsey was a member of an external committee that assessed my work, as a sort of tenure review. I will always be grateful for the positive feedback I received, although it was to no avail because budget cuts and a hiring freeze led to my leaving NIH in 1995. Plonsey retired from Duke in 1996, and our paths didn’t cross again. He was a gracious gentleman who I will always have enormous respect for. Indeed, the first seven years of my professional life were spent traveling down a path parallel to and often intersecting his; to put it more aptly, I was dashing down a trail he had blazed.
Robert Plonsey was a World War Two veteran (we are losing them too fast these days), and a leader in establishing biomedical engineering as an academic discipline. You can read his obituary here and here.
I will miss him.
Subscribe to:
Posts (Atom)