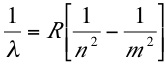A Dangerous Error in the Dilution of 25 Percent Albumin

In Problem 5 in Chapter 5 of the 4th edition of Intermediate Physics for Medicine and Biology, Russ Hobbie and I consider what happens if a drug is administered without carefully considering osmotic effects. The problem refers to a letter to the editor in the New England Journal of Medicine from Donald Steinmuller.

A Dangerous Error in the Dilution of 25 Percent Albumin

To the Editor: Physicians and pharmacists should be alert to a serious error that can occur in the preparation of replacement albumin solutions for plasmapheresis.

Plasmapheresis was performed in an elderly man who had myeloma with renal insufficiency. One plasma volume exchange was ordered, with 5 percent albumin as the replacement solution, with calcium, potassium, and magnesium supplements. Because of the lack of availability of 5 percent albumin, the hospital pharmacy used 25 percent albumin and diluted this solution 1:4 with sterile water to achieve a 5 percent solution. Reference was made to Trissel’s Handbook on Injectable Drugs, the 1994 edition of which states, “A 5% solution may be prepared from the 25% product by adding 1 volume of the 25% albumin to 4 volumes of sterile water or an infusion solution such as dextrose 5% in water or sodium chloride 0.9%.” The pharmacist used sterile water as described by the handbook, resulting in a hypo-osmolar solution that caused severe hemolysis in the patient. The hematocrit dropped 7.3 points, and renal failure developed.

This flagrant error in instructing dilution with water was only partially corrected in the 1996 edition of Trissel's handbook. This edition states, “If sterile water for injection is the diluent, the tonicity of the diluted solution must be considered. Substantial reduction in tonicity creates the potential for hemolysis.” In view of the osmolarity of the 25 percent albumin solution diluted with sterile water (approximately 36 mOsm per liter), one should never use water to dilute 25 percent albumin.

The problem is aggravated by the label on the 25 percent albumin solution. The label states that 100 ml of 25 percent albumin is “osmotically equivalent to 500 ml of plasma.” This statement is not true. It confuses the osmotic and oncotic effects. The oncotic effect of 100 ml of the 25 percent solution is equivalent to 500 ml of plasma, but since the concentration of saline in the 25 percent solution is isotonic with plasma, the osmotic effect of 100 ml of the 25 percent is equivalent to only 100 ml of plasma.

The handbook and product label need to be corrected as soon as possible to prevent this error in the future. Pharmacies and the medical community should be alert to this potentially life-threatening error.

This letter makes the distinction between osmotic pressure and oncotic pressure, that part of the osmotic pressure caused by large colloidal particles such as albumin.

Before publication, the editor sent the letter to experts at the FDA, who responded with a separate letter that immediately followed Steinmuller’s

…Including the case reported by Dr. Steinmuller, the FDA is aware of four cases of hemolysis that have occurred since 1994 during or after plasmapheresis when albumin (human) 25 percent was diluted to a 5 percent solution with the use of sterile water for injection…. The FDA has taken the following steps to advise the medical community of this potentially serious problem. First, the FDA is recommending to manufacturers of albumin (human) 25 percent that the package inserts for their products be revised to include … information on acceptable diluents, such as 0.9 percent sodium chloride or 5 percent dextrose in water…

The FDA letter triggered a third letter from Richard Kravath, of Kings County Hospital Center in Brooklyn

…Although the response by the representatives of the Food and Drug Administration (FDA) is correct with regard to the recommendation that dilution with 5 percent glucose, instead of water alone, would prevent hemolysis, use of this solution would not prevent the possible development of hyponatremia and brain swelling if the solution were used rapidly in large volumes, as in plasma exchange. Owing to its oncotic pressure, the albumin would tend to remain in the plasma compartment, whereas the glucose would rapidly leave the circulation, enter the interstitial fluid and then enter cells, become metabolized, and no longer exert an osmotic effect….

Glucose solutions should not be used to replace plasma or other extracellular fluids. Sodium chloride 0.9 percent (154 mmol per liter) is a reasonable alternative, but a more physiologic solution, one that more closely resembles plasma, would be even better.

The authors of the handbook quoted by Steinmuller also wrote a letter, in which they quoted the corrected 9th edition of their book (Steinmuller had cited the 8th edition) and claimed (somewhat lamely, in my opinion) that “…It is common knowledge that large volumes of very hypotonic solutions should not be administered intravenously….” and “…This situation points to the need for health care practitioners to use up-to-date references...”.

Finally, the FDA experts responded to these last two letters.

…Plasma exchange or plasmapheresis represents a unique circumstance because, in formulating the replacement solution, one must take into account not only the loss of endogenous plasma proteins (principally, but not exclusively, albumin) but also the fact that significant quantities of electrolytes such as sodium and chloride are being removed by the procedure...

This exchange of letters is fascinating, and emphasizes the importance of the osmotic effects that Russ and I discuss in Chapter 5. The original letter by Steinmuller, which highlights an important medical issue, also makes for an instructive homework problem.

Let me conclude by noting an error (now listed in the book errata, downloadable at the book website) in the 4th edition of Intermediate Physics for Medicine and Biology. Russ and I have the title of Steimnuller’s letter incorrect. On page 133 we write “15 percent” when the title of the letter actually says “25 percent”. The homework problem correctly uses 25 %, and needs no change. Below is the corrected citation:

Steinmuller, D. R. (1998) “A Dangerous Error in the Dilution of 25 Percent Albumin,” New England Journal of Medicine, Volume 338, Page 1226.

Marie Curie

Marie Curie (1867–1934) is one of the few scientists who received two Nobel Prizes: for Physics in 1903, and for Chemistry in 1911. Russ Hobbie and I don’t discuss Curie extensively in the 4th edition of Intermediate Physics for Medicine and Biology, but in Chapter 17 on Nuclear Medicine we do introduce the unit of radioactive activity named for her.

The activity A(t) is the number of radioactive transitions (or transformations or disintegrations) per second. The SI unit of activity is the becquerel (Bq):

1 Bq = 1 transition s⁻¹.

The earlier unit of activity, which is still used occasionally, is the curie (Ci):

1 Ci=3.7 × 10¹⁰ Bq,

1 μCi = 3.7 ×10⁴ Bq.

Several excellent articles were published about Marie Curie and her husband/collaborator Pierre Curie for the centennial of her 1898 discovery of radium. Saenger and Adamek’s article in the journal Medical Physics states

Marie Curie’s activities and research left her imprint on nuclear medicine, which continues to this day. Much of her impact is related to the role of women in science, biology, and medicine. She successfully overcame struggles for recognition in the first decades of this century. One of her major achievements was the development of field-radiography for wounded soldiers in World War I. Her continued endeavors to provide radium therapy for cancer was a giant step for humanity. She worked unceasingly in the laboratory to separate and identify radioactive elements of the periodic table. The standardization of these elements resulted in the 1931 report of the International Radium-Standards Commission and the posthumous two-volume Radio-aktivite´.

The abstract of Mould’s article in the British Journal of Radiology begins

This review celebrates the events of 100 years ago to the month of publication of this December 1998 issue of the British Journal of Radiology, when radium was discovered by the Curies. This followed the earlier discovery in November 1895 of X-rays by Röntgen, which has already been reviewed in the British Journal of Radiology [1] and the discovery in March 1896, by Becquerel, of the phenomenon of radioactivity, which introduces this review. This is particularly relevant as Marie Curie was in 1897 a research student in Becquerel’s laboratory. Marie Curie’s life in Poland prior to her 1891 departure for Paris is included in this review as are other aspects of her life and work such as her work in World War I with radiological ambulances (known as “Little Curies”) on the battlefields of France and Belgium, early experiments with radium and the founding of the Institut du Radium in Paris and of the Radium Institute in Warsaw. Wherever possible I have included appropriate quotations in Marie Curie’s own words [2–4] and each section is related in some way to the life and work of Maria or Pierre. This review is completed with details of the re-interment of the bodies of Pierre and Marie on 20 April 1995 in The Panthéon, Paris.

Excellent overviews of Curie’s life and work are provided by the AIP Center for the History of Physics and the Official Website of the Nobel Prize. You can read about the discovery of radium in Maria Curie’s own words here. And for all you dear readers who prefer Saturday morning cartoons to learned articles, watch this; it doesn’t include any complex or controversial stuff like the Langevin affair, but it is enjoyable in its own simple way.

Marie Curie Animated Hero Classics
https://www.youtube.com/watch?v=x-ynt1yY43I&t=205s

Recently, the visual artist/filmmaker/writer Quintan Ana Wikswo was granted access to Marie Curie’s laboratory in Paris for “creating performance films and photographs for ... LUMINOSITY: THE PASSIONS OF MARIE CURIE, a multimedia opera by composer Pamela Madsen.” Wikswo describes her ongoing work and previews some of her photographs in her blog Bumblemoth.

To see her books, her equipment, to stand at her desk, to see her beakers and centrifuges and shelves of chemicals…it’s a kind of searing existential therapy, and anyone visiting Paris should make the effort to spend a few moments at her lab. Why? It’s an antidote, at the very least. I work half-days at her lab, and then explore art museums of Paris in the off hours. The contrast is shocking and disturbing. Inspiring and sorrowful.

At Oakland University, I work in the College of “Arts and Sciences.” Wikswo has found her own niche at the intersection of these two rarely-overlapping endeavors. I look forward to seeing the completed project.

The Sinogram

I love sinograms. They are rare and fascinating mixtures of science and art, and often are quite beautiful. One should be able to look at a sinogram and intuitively picture the two-dimensional image. Unfortunately, I rarely can do this, except for the most simple examples.

Russ Hobbie and I define the sinogram in the 4th edition of Intermediate Physics for Medicine and Biology. We explain how to calculate the projection, F(θ, x'), from the image, f(x,y). This transformation and its inverse—determining f(x,y) from F(θ,x')—is at the heart of many imaging algorithms, such as those used in computed tomography.

The process of calculating F(θ, x') from f(x, y) is sometimes called the Radon transformation. When F(θ, x') is plotted with x’ on the horizontal axis, θ on the vertical axis, and F as the brightness or height on a third perpendicular axis, the resulting picture is called a sinogram. For example, the projection of f(x, y) = δ(x − x₀)δ(y − y₀) is F(θ, x') = δ(x' − (x₀ cos θ + y₀ sin θ)). A plot of this object and its sinogram is shown in Fig. 12.17.

Figure 12.17 does indeed contain a sinogram, but a very simple one: the sinogram of a point is just a sine wave. The reader is asked to produce a somewhat more complicated sinogram in homework Problem 29.

Problem 29 An object consists of three δ functions at (0, 2), (√3,−1), and (−√3,−1). Draw the sinogram of the object.

This sinogram consists of three braided sine waves. I like this example, because it’s simple enough that you the reader should be able to reason out the structure of the sinogram by imagining the projection in your head, but it is complicated enough that it’s not trivial.

When preparing the 4th edition of Intermediate Physics for Medicine and Biology, I derived a couple new homework problems (Chapter 12, Problems 23 and 24) for which the inverse transformation can be solved analytically. I think these are useful exercises that build intuition with the Fourier transform method of reconstructing an image (see Fig. 12.20, top path). It occurs to me now, however, that while these problems do provide insight and practice for the mathematically inclined reader, they also offer the opportunity to further illustrate the sinogram. So this week I made the figures below, showing the image f(x,y) on the left and the corresponding sinogram F(θ,x') on the right, for the functions in Problems 23 and 24.

Problem 23.

Problem 24.

Let us try to interpret these pictures qualitatively. The vertical axis in the sinogram (right panel) indicates the angle, specifying the direction of the projection (the direction that the x-rays come from, to use CT terminology). The bottom of the θ axis is an angle of zero indicating x-rays are incident on the image from the bottom, the middle of the θ axis is x-rays incident from the left, and the top of the θ axis is x-rays incident from the top (see Fig. 12.12). Some authors extend the θ axis so it ranges from 0 to 360°, but to me that seems unnecessary since having the x-rays come from one side or the opposite side does not matter; it provides no new information. It’s best if you, dear reader, pause now and stare at these sinograms until you understand how they relate to the image. If you really want to build your intuition, cover the left panel, and try to predict what the hidden image looks like from just the right panel. Or, solve homework Problems 30 and 31 in Chapter 12, and then plot both the image and its sinogram like I do above.

This website has some nice examples of sinograms. For instance, a sinogram of a line is just a point. Think about it and sketch some projections to convince yourself this is correct. Also this website shows a sinogram of a square located away from the center of the image (it looks like the sinogram above for Fig. 23, but with interesting bright curves tenuously weaving throughout the sinogram arising from the corners of the square). Finally, the website shows the sinogram of an image known as a Shepp-Logan head phantom. (Warning, the website displays its sinograms rotated by 90° compared to the way Russ and I plot them; it plots the angle along the horizontal axis.) The video shown below provides additional insight into the construction of the sinogram for the Shepp-Logan head phantom.

Here is one of my favorite images: a detailed image of a brain, and its lovely sinogram. If you can do the inverse transformation of this complicated sinogram in your head, you’re a better medical physicist than I am. 

An image of a brain, and its sinogram,
adapted from Wikipedia.

The Hydrogen Spectrum

One of the greatest accomplishments of atomic physics is Neils Bohr’s model for the structure of the hydrogen atom, and his prediction of the hydrogen spectrum. While Bohr gets the credit for deriving the formula for the wavelengths, λ, of light emitted by hydrogen—one of the early triumphs of quantum mechanics—it was first discovered empirically from the spectroscopic analysis of Johannes Rydberg. In the 4th edition of Intermediate Physics for Medicine and Biology, Russ Hobbie and I introduce Rydberg’s formula in Homework Problem 4 of Chapter 14.

Problem 4 (a) Starting with Eq. 14.7, derive a formula for the hydrogen atom spectrum in the form

where n and m are integers. R is called the Rydberg constant. Find an expression for R in terms of fundamental constants. 

(b) Verify that the wavelengths of the spectral lines a-d at the top of Fig. 14.3 are consistent with the energy transitions shown at the bottom of the figure.

Our Fig. 14.3 is in black and white. It is often useful to see the visible hydrogen spectrum (just four lines, b-e in Fig 14.3) in color, so you can appreciate better the position of the emission lines in the spectrum.

(Figure from http://chemed.chem.purdue.edu/genchem/topicreview/bp/ch6/graphics/hydrogen.gif).

The hydrogen lines in the visible part of the spectrum are often referred to as the Balmer series, in honor of physicist Johann Balmer who discovered this part of the spectrum before Rydberg. Additional Balmer series lines exist in the near ultraviolet part of the spectrum (the thick band of lines just to the left of line e at the top of Fig. 14.3). All the Balmer series lines can be reproduced using the equation in Problem 4 with n = 2.

An entire series of spectral lines exists in the extreme ultraviolet, called the Lyman series, shown at the top of Fig. 14.3 as the line labeled a and the lines to its left. These lines are generated by the formula in Problem 4 using n = 1. The new homework problem below will help the student better understand the hydrogen spectrum.

Section 14.2

Problem 4 ½ The Lyman series, part of the spectrum of hydrogen, is shown at the top of Fig. 14.3 as the line labeled a and the band of lines to the left of that line. Create a figure like Fig. 14.3, but which shows a detailed view of the Lyman series. Let the wavelength scale at the top of your figure range from 0 to 150 nm, as opposed to 0-2 μm in Fig. 14.3. Also include an energy level drawing like at the bottom of Fig. 14.3, in which you indicate which transitions correspond to which lines in the Lyman spectrum. Be sure to indicate the shortest possible wavelength in the Lyman spectrum, show what transition that wavelength corresponds to, and determine how this wavelength is related to the Rydberg constant.

Many spectral lines can be found in the infrared, known as the Paschen series (n = 3), the Brackett series (n = 4) and the Pfund series (n = 5). The Paschen series is shown as lines f, g, h, and i in Fig. 14.3, plus the several unlabeled lines to their left. The Paschen, Brackett, and Pfund series overlap, making the hydrogen infrared spectrum more complicated than its visible and ultraviolet spectra. In fact, the short-wavelength lines of the Brackett series would appear at the top of Fig. 14.3 if all spectral lines were shown.

Asimov's Biographical Encyclopedia
of Science and Technology,
by Isaac Asimov.

Rydberg’s formula, given in Problem 4, nicely summarizes the entire hydrogen spectrum. Johannes Rydberg is a Swedish physicist (I am 3/8th Swedish myself). His entry in Asimov's Biographical Encyclopedia of Science and Technology reads

RYDBERG, Johannes Robert (rid’bar-yeh) Swedish physicist Born: Halmstad, November 8, 1854. Died: Lund, Malmohus, December 28, 1919.

Rydberg studied at the University of Lund and received his Ph.D. in mathematics in 1879, and then jointed the faculty, reaching professorial status in 1897.

He was primarily interested in spectroscopy and labored to make sense of the various spectral lines produced by the different elements when incandescent (as Balmer did for hydrogen in 1885). Rydberg worked out a relationship before he learned of Balmer’s equation, and when that was called to his attention, he was able to demonstrate that Balmer’s equation was a special case of the more general relationship he himself had worked out.

Even Rydberg’s equation was purely empirical. He did not manage to work out the reason why the equation existed. That had to await Bohr’s application of quantum notions to atomic structure. Rydberg did, however, suspect the existence or regularities in the list of elements that were simpler and more regular than the atomic weights and this notion was borne out magnificently by Moseley’s elucidation of atomic numbers.

Yesterday was the 158th anniversary of Rydberg’s birth.

Art Winfree and Cellular Excitable Media

When Time Breaks Down,
by Art Winfree.

Ten years ago Art Winfree died. I’ve written about Winfree in this blog before (for example, see here, and here). He shows up often in the 4th edition of Intermediate Physics for Medicine and Biology; Russ Hobbie and I cite Winfree’s research throughout our discussion of nonlinear dynamics and cardiac electrophysiology.

One place where Winfree’s work impacts our book is in Problems 39 and 40 in Chapter 10, discussing cellular automata. Winfree didn’t invent cellular automata, but his discussion of them in his wonderful book When Time Breaks Down is where I first learned about the topic.

Box 5.A: A Cellular Excitable Medium

Take a pencil and a sheet of tracing paper and play with Figure 5.2 [a large hexagonal array of cells] according to the following game rules … Each little hexagon in this honeycomb is supposed to represent a cell that may be excited for the duration of one step (put a “0” in the cell) or refractory (after the excited moment, replace the “0” with a “1”) or quiescent (after that erase the “1”) until such time as any adjacent cell becomes excited: then pencil in a “0” in the next step.

If you start with no “0’s,” you’ll never get any, and this simulation will cost you little effort. If you start with a single “0” somewhere, it will next turn to “1” while a ring of 6 neighbors become infected with “0”. As the hexagonal ring of “0’s” propagates, it is followed by a concentric ring of “1” refractoriness, right to the edge of the honeycomb, where all vanish.

Now see what happens if you violate the rules just once by erasing a segment of that ring wave when it is about halfway to the edges: you will have created a pair of counter-rotating vortices (alias phase singularities), each of which turns out to be a source of radially propagating waves.

(Stop reading until you have played some.)

You may feel a bit foolish, since this is obviously supposed to mimic action potential propagation, and the caricature is embarrassingly crude. Which aspects of its behavior are realistic and which others are merely telling us “honeycombs are not heart muscle”? The way to find out is to undertake successively more refined caricatures until a point of diminishing returns is reached. For most purposes, it is reached surprisingly soon.

I consider cellular automata—whose three simple rules can be mastered by a child—to be among the best tools for illustrating cardiac reentry. I like this model so much that I generalized it to account for electrical simulation that produces adjacent regions of depolarization and hyperpolarization (Sepulveda et al., 1989; read more about that paper here). In “Virtual Electrodes Made Simple: A Cellular Excitable Medium Modified for Strong Electrical Stimuli,” published in the Online Journal of Cardiology, I added a fourth rule

During a cathodal stimulus, the state of the cell directly under the electrode and its four nearest neighbors in the direction perpendicular to the fibers change to the excited state, and the two remaining nearest neighbors in the direction parallel to the fibers change to the quiescent state, regardless of their previous state.

Using this simple model, I was able to initiate “quatrefoil reentry” (Lin et al., 1999; read more here). I also could reproduce most of the results of a simulation of the “pinwheel experiment” (a point stimulus applied near the end of the refractory period of a previous planar wave front) predicted by Lindblom et al. (2000). I concluded

This extremely simple cellular excitable medium—which is nothing more than a toy model, stripped down to contain only the essential features—can, with one simple modification for strong stimuli, predict many interesting and important phenomena. Much of what we have learned about virtual electrodes and deexcitation is predicted correctly by the model (Efimov et al., 2000; Trayanova, 2001). I am astounded that this simple model can reproduce the complex results obtained by Lindblom et al. (2000). The model provides valuable insight into the essential mechanisms of electrical stimulation without hiding the important features behind distracting details.

My online paper came out in 2002, the same year that Winfree died. In an obituary, Steven Strogatz wrote

When Art Winfree died in Tucson on November 5, 2002, at the age of 60, the world lost one of its most creative scientists. I think he would have liked that simple description: scientist. After all, he made it nearly impossible to categorize him any more precisely than that. He started out as an engineering physics major at Cornell (1965), but then swerved into biology, receiving his PhD from Princeton in 1970. Later, he held faculty positions in theoretical biology (Chicago, 1969–72), in the biological sciences (Purdue, 1972–1986), and in ecology and evolutionary biology (University of Arizona, from 1986 until his death).

So the eventual consensus was that he was a theoretical biologist. That was how the MacArthur Foundation saw him when it awarded him one of its “genius” grants (1984), in recognition of his work on biological rhythms. But then the cardiologists also claimed him as one of their own, with the Einthoven Prize (1989) for his insights about the causes of ventricular fibrillation. And to further muddy the waters, our own community honored his achievements with the 2000 AMS-SIAM Norbert Wiener Prize in Applied Mathematics, which he shared with Alexandre Chorin.

Aside from his versatility, what made Winfree so special (and in this way he was reminiscent of Wiener himself) was the originality of the problems he tackled; the sparkling creativity of his methods and results; and his knack for uncovering deep connections among previously unrelated parts of science, often guided by geometrical arguments and analogies, and often resulting in new lines of mathematical inquiry.