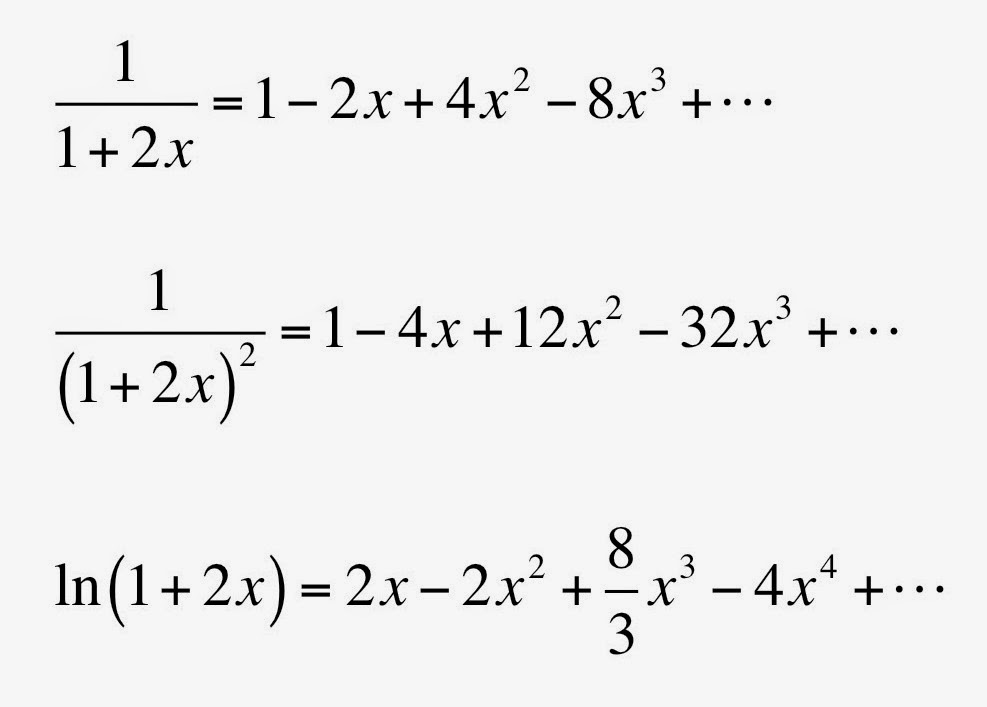Turing was primarily a mathematician, but he did publish one paper that straddled the disciplines of mathematical biology and biological physics: A. M. Turing, 1952, “Chemical Basis of Morphogenesis.” Philosophical Transactions of the Royal Society of London. Series B, Volume 237, Pages 37–72. The abstract is reproduced below.
It is suggested that a system of chemical substances, called morphogens, reacting together and diffusing through a tissue, is adequate to account for the main phenomena of morphogenesis. Such a system, although it may originally be quite homogeneous, may later develop a pattern or structure due to an instability of the homogeneous equilibrium, which is triggered off by random disturbances. Such reaction-diffusion systems are considered in some detail in the case of an isolated ring of cells, a mathematically convenient, though biologically unusual system. The investigation is chiefly concerned with the onset of instability. It is found that there are six essentially different forms which this may take. In the most interesting form stationary waves appear on the ring. It is suggested that this might account, for instance, for the tentacle patterns on Hydra and for whorled leaves. A system of reactions and diffusion on a sphere is also considered. Such a system appears to account for gastrulation. Another reaction system in two dimensions gives rise to patterns reminiscent of dappling. It is also suggested that stationary waves in two dimensions could account for the phenomena of phyllotaxis. The purpose of this paper is to discuss a possible mechanism by which the genes of a zygote may determine the anatomical structure of the resulting organism. The theory does not make any new hypotheses; it merely suggests that certain well-known physical laws are sufficient to account for many of the facts. The full understanding of the paper requires a good knowledge of mathematics, some biology, and some elementary chemistry. Since readers cannot be expected to be experts in all of these subjects, a number of elementary facts are explained, which can be found in text-books, but whose omission would make the paper difficult reading.
 |
| Mathematical Biology, by James Murray. |
Turing’s (1952) idea is a simple but profound one. He said that if, in the absence of diffusion….[two chemicals] A and B tend to a linearly stable uniform steady state then, under certain conditions, which we shall derive, spatially inhomogeneous patterns can evolve by diffusion driven instability… Diffusion is usually considered a stabalising process which is why this was such a novel concept. To see intuitively how diffusion can be destabilizing consider the following, albeit unrealistic, but informative analogy.I don’t know about you, but I gotta love someone who explains mathematics using dry grass and grasshoppers.
Consider a field of dry grass in which there is a large number of grasshoppers…
Diffusion is a key concept underlying Turing’s work. Russ Hobbie and I discussion diffusion in Chapter 4 of the 4th edition of Intermediate Physics for Medicine and Biology, and it is one of the central ideas in all of biological physics. Diffusion-driven instabilities play a role when analyzing the Belousov-Zhabotinsky oscillating chemical reaction, and are relevant to explaining how leopards get their spots (a spotted leopard graces the cover of Murray’s book; whenever I search for his book in the stacks of the OU library, I just look for the leopard).
Murray continues
A reaction diffusion system exhibits diffusion-driven instability or Turing instability if the homogeneous stead state is stable to small perturbations in the absence of diffusion but unstable to small spatial perturbations when diffusion is present. The usual concept of instability in biology is in the context of ecology, where a uniform steady state becomes unstable to small perturbations and the populations typically exhibit some temporal oscillatory behaviour. The instability we are concerned with here is of a quite different kind. The mechanism driving the spatially inhomogeneous instability is diffusion: the mechanism determines the spatial pattern that evolves. How the pattern or mode is selected is an important aspect of the analysis.Not only did Turing make a monumental contribution to deciphering the enigma code, but also he helped to develop the field of mathematical biology. In my book, that makes him a biological physicist.