Terminal Speed of Microorganisms

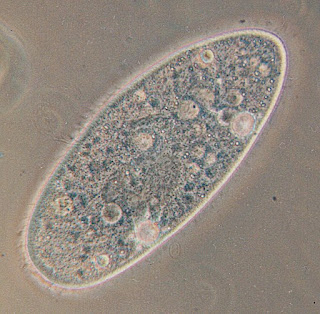
A Paramecium aurelia seen through an optical microscope.
Source: Wikipedia (http://en.wikipedia.org/wiki/Image:Paramecium.jpg)

Homework Problem 28 at the end of Chapter 2 in Intermediate Physics for Medicine and Biology asks the reader to calculate the terminal speed of an animal falling in air. Although this problem provides insight, it includes a questionable assumption. Russ and I tell the student to “assume that the frictional force is proportional to the surface area of the animal.” If, however, the animal falls at low Reynolds number, this assumption is not valid. Instead, the drag force is given by Stokes’ law, which is proportional to the radius, not the surface area (radius squared). The new homework problem given below asks the reader to calculate the terminal speed for a microorganism falling through water at low Reynolds number.

Section 2.8

Problem 28 ½. Calculate the terminal speed, V, of a paramecium sinking in water. Assume that the organism is spherical with radius R, and that the Reynolds number is small so that the drag force is given by Stokes’ law. Include the effect of buoyancy. Let the paramecium’s radius be 100 microns and its specific gravity be 1.05. Verify that its Reynolds number is small.

The reader will first need to get the density ρ and viscosity η of water, which are ρ = 1000 kg/m³ and η = 0.001 kg/(m s). The specific gravity is not defined in IPMB, but it’s the density divided by the density of water, implying that the density of the paramecium is 1050 kg/m³. Finally, Stokes’ law is given in IPMB as Eq. 4.17, F_drag = –6πRηV.

I’ll let you do your own calculation. I calculate the terminal speed to be about 1 mm/s, so it takes about a fifth of a second to sink one body diameter. The Reynolds number is 0.1, which is small, but not exceptionally small.

You should find that the terminal speed increases as the radius squared, in contrast to a drag force proportional to the surface area for which the terminal speed increases in proportion to the radius. Bigger organisms sink faster. The dependence of terminal speed on size is even more dramatic for aquatic microorganisms than for mammals falling in air. To paraphrase Haldane’s quip, “a bacterium is killed, a diatom is broken, a paramecium splashes,” except the speeds are small enough that none of the “wee little beasties” are really killed (the terminal speed is not terminal...get it?) and splashing is a high Reynolds number phenomenon.

Buoyancy is not negligible for aquatic animals. The effective density of a paramecium in air would be about 1000 kg/m³, but in water its effective density drops to a mere 50 kg/m³. Microorganisms are made mostly of water, so they are almost neutrally buoyant. In this homework problem, the effect of gravity is reduced to only five percent of what it would be if buoyancy were ignored.

A paramecium is a good enough swimmer that it can swim upward against gravity if it wants to. Its surface is covered with cilia that beat together like a Roman galley to produce the swimming motion (ramming speed!).

Whenever discussing terminal speed, one should remember that we assume the fluid is initially at rest. In fact, almost any volume of water will have currents moving at speeds greater than 1 mm/s, caused by tides, gravity, thermal convection, wind driven waves, or the wake of a fish swimming by. A paramecium would drift along with these currents. To observe the motion described in this new homework problem, one must be careful to avoid any bulk movement of water.

If you watched a paramecium sink in still water, would you notice any Brownian motion? You can calculate the root-mean-squared thermal speed with Eq. 4.12 in IPMB, using the mass of the paramecium as four micrograms and a temperature of 20° C. You get approximately 0.002 mm/s. That is less than 1% of the terminal speed, so you wouldn’t notice any random Brownian motion unless you measured extraordinarily carefully.