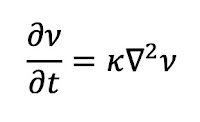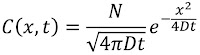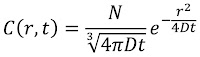Problem 20. People use many cues to estimate the direction a sound came from. One is the time delay between sound arriving at the left and right ears. Estimate the maximum time delay. Ignore any diffraction effects caused by the head.
 |
| Air and Water, by Mark Denny. |
Sense the Direction that Fluid Moves in a Sound Wave
Some animals can sense the direction that fluid moves in a sounds wave. This requires an ear that responds to motion (a vector) instead of pressure (a scalar). Apparently this ability is common in fish, but not in terrestrial animals.Comparing the Intensity at Each Ear
Most animals have two ears. If one is closer to the source of a sound than the other, it hears a louder sound. Also, the presence of the body may attenuate or diffract the sound that reaches the far ear, changing its intensity. Denny notes two problems with this mechanism. First, attenuation in air occurs over large distances (70 dB per kilometer), so we would not expect much difference of intensity because the ears are, say, 20 cm apart. Second, the perceived direction is ambiguous. The sound from a source in front of us produces the same intensity at each ear, but so does sound from a source behind us. One way to resolve the ambiguity is to tilt your head as you listen, providing two data point: before and after the tilt.Comparing the Delay at Each Ear
The homework problem Russ and I wrote is based on the time difference of sound arriving at each ear. This mechanism shares the problem mentioned earlier of direction ambiguity. The biggest problem, however, is that the arrival time at each ear differs by only a small amount: less than a millisecond. Nevertheless, bats appear to make use of this mechanism. For smaller animals (such as hummingbirds) the delays may be too short to be perceptible. Moreover, the speed of sound in water is more than four times the speed of sound in air, so this mechanism is unreliable for aquatic animals. SCUBA divers have trouble localizing sound.Detecting the Phase Shift Between Each Ear
This mechanism is similar to comparing arrival times, except instead of sensing the delay you sense the phase difference. The method suffers from the same ambiguities discussed earlier, plus another unique to the detection of phase. If the phase shifts by an entire wavelength, it sounds the same as if it had no phase shift at all. So, you don’t want large phase shifts (greater than 2π), but you don’t want small phase shifts that are lost in the noise. Some small animals (such as crickets) have their ears connected by an air-filled tube, so they only detect sound when the two ears are out of phase. Because the speed of sound changes with temperature, any mechanism based on the speed of sound might function differently on a cold day than on a hot one.Denny concludes
Despite the inherent problems of determining direction, animals combine the methods described above and thereby perform admirably. For example, bats and owls have been shown to localize sounds with 1° to 2°, and dolphins have similar directional acuity. Humans, cats, and opossums can localize sounds within 1° to 6° (Lewis 1983). These abilities are a tribute to the ability of the nervous system to assimilate complex data.I don’t mind being beaten out by a cat, but we humans need to up our game if we want to do better than those possums.