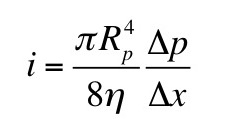Mathematical Physiology

Mathematical Physiology,
by James Keener and James Sneyd.

In a comment to the blog last week, Frankie mentioned the two-volume textbook Mathematical Physiology (MP), by James Keener and James Sneyd. Russ Hobbie and I cite Keener and Sneyd in Chapter 10 (Feedback and Control) of Intermediate Physics for Medicine and Biology. The Preface to the first edition of MP begins:

It can be argued that of all the biological sciences, physiology is the one in which mathematics has played the greatest role. From the work of Helmholtz and Frank in the last century through to that of Hodgkin, Huxley, and many others in this century [the first edition of MP was published in 1998], physiologists have repeatedly used mathematical methods and models to help their understanding of physiological processes. It might thus be expected that a close connection between applied mathematics and physiology would have developed naturally, but unfortunately, until recently, such has not been the case.

There are always barriers to communication between disciplines. Despite the quantitative nature of their subject, many physiologists seek only verbal descriptions, naming and learning the functions of an incredibly complicated array of components; often the complexity of the problem appears to preclude a mathematical description. Others want to become physicians, and so have little time for mathematics other than to learn about drug dosages, office accounting practices, and malpractice liability. Still others choose to study physiology precisely because thereby they hope not to study more mathematics, and that in itself is a significant benefit. On the other hand, many applied mathematicians are concerned with theoretical results, proving theorems and such, and prefer not to pay attention to real data or the applications of their results. Others hesitate to jump into a new discipline, with all its required background reading and its own history of modeling that must be learned.

But times are changing, and it is rapidly becoming apparent that applied mathematics and physiology have a great deal to offer one another. It is our view that teaching physiology without a mathematical description of the underlying dynamical processes is like teaching planetary motion to physicists without mentioning or using Kepler’s laws; you can observe that there is a full moon every 28 days, but without Kepler’s laws you cannot determine when the next total lunar or solar eclipse will be nor when Halley’s comet will return. Your head will be full of interesting and important facts, but it is difficult to organize those facts unless they are given a quantitative description. Similarly, if applied mathematicians were to ignore physiology, they would be losing the opportunity to study an extremely rich and interesting field of science.

To explain the goals of this book, it is most convenient to begin by emphasizing what this book is not; it is not a physiology book, and neither is it a mathematics book. Any reader who is seriously interested in learning physiology would be well advised to consult an introductory physiology book such as Guyton and Hall (1996) or Berne and Levy (1993), as, indeed, we ourselves have done many times. We give only a brief background for each physiological problem we discuss, certainly not enough to satisfy a real physiologist. Neither is this a book for learning mathematics. Of course, a great deal of mathematics is used throughout, but any reader who is not already familiar with the basic techniques would again be well advised to learn the material elsewhere.

Instead, this book describes work that lies on the border between mathematics and physiology; it describes ways in which mathematics may be used to give insight into physiological questions, and how physiological questions can, in turn, lead to new mathematical problems. In this sense, it is truly an interdisciplinary text, which, we hope, will be appreciated by physiologists interested in theoretical approaches to their subject as well as by mathematicians interested in learning new areas of application.

If you substitute the words “physics” for “mathematics,” “physical” for “mathematical,” and “physicist” for “mathematician,” you would almost think that this preface had been written by Russ Hobbie for an early edition of IPMB.

Many of the topics in MP overlap those in IPMB: diffusion, bioelectricity, osmosis, ion channels, blood flow, and the heart. MP covers additional topics not in IPMB, such as biochemical reactions, calcium dynamics, bursting pancreatic beta cells, and the regulation of gene expression. What IPMB has that MP doesn’t is clinical medical physics: ultrasound, x-rays, tomography, nuclear medicine, and MRI. Both books assume a knowledge of calculus, both average many equations per page, and both have generous collections of homework problems.

Which book should you use? Mathematical Physiology won an award, but Intermediate Physics for Medicine and Biology has an award-winning blog. I’ll take the book with the blog. I bet I know what Frankie will say: “I’ll take both!”

I Spy Physiology

Last year I wrote a blog post about learning biology, aimed at physicists who wanted an introduction to biological ideas. Today, let’s suppose you have completed your introduction to biology. What’s next? Physiology!

What is physiology? Here is the answer provided by the website physiologyinfo.org, sponsored by the American Physiological Society.

Physiology is the study of how the human body works under normal conditions. You use physiology when you exercise, read, breathe, eat, sleep, move or do just about anything.

Physiology is generally divided into ten physiological organ systems: the cardiovascular system, the respiratory system, the immune system, the endocrine system, the digestive system, the nervous system, the renal system, the muscular system, the skeletal system, and the reproductive system.

Screenshot of the I Spy Physiology website.

My favorite part of physiologyinfo.org is the I Spy Physiology blog.

At the American Physiological Society (APS), we believe that physiology is everywhere. It is the foundational science that provides the backbone to our understanding of health and medicine. At its core, physiology is all about understanding the healthy (normal) state of animals—humans included!—what happens when something goes wrong (the abnormal state) and how to get things back to working order. Physiologists study these normal and abnormal states at all levels of the organism: from tiny settings like in a cell to large ones like the whole animal. We also study how humans and animals function, including how they eat, breathe, survive, exercise, heal and sense the environment around them.

On this blog, we’ll endeavor to answer the questions “What is physiology?”, “Where is physiology?”, and “Why does it matter to you?” through current news and health articles and research snippets highlighted by APS members and staff. We’ll also explore the multifaceted world of physiology and follow the path from the lab all the way to the healthy lifestyle recommendations that you receive from your doctor

Other parts of the website I like are “Quizzes and Polls” (I aced the cardiovascular system quiz!) and the podcast library. As a Michigander, I was pleased to see the article about William Beaumont. Finally, I enjoyed Dr. Dolittle’s delightful blog Life Lines, about comparative physiology.

My only complaint about physiologyinfo.org is its lack of physics. That is where Intermediate Physics for Medicine and Biology comes in: IPMB puts the physics in the physiology.

dGEMRIC

dGEMRIC is an acronym for delayed gadolinium enhanced magnetic resonance imaging of cartilage. Adil Bashir and his colleagues provide a clear introduction to dGEMRIC in the abstract of their paper “Nondestructive Imaging of Human Cartilage Glycosaminoglycan Concentration by MRI” (Magnetic Resonance in Medicine, Volume 41, Pages 857–865, 1999).

Despite the compelling need mandated by the prevalence and morbidity of degenerative cartilage diseases, it is extremely difficult to study disease progression and therapeutic efficacy, either in vitro or in vivo (clinically). This is partly because no techniques have been available for nondestructively visualizing the distribution of functionally important macromolecules in living cartilage. Here we describe and validate a technique to image the glycosaminoglycan concentration ([GAG]) of human cartilage nondestructively by magnetic resonance imaging (MRI). The technique is based on the premise that the negatively charged contrast agent gadolinium diethylene triamine pentaacetic acid (Gd(DTPA)^2-) will distribute in cartilage in inverse relation to the negatively charged GAG concentration. Nuclear magnetic resonance spectroscopy studies of cartilage explants demonstrated that there was an approximately linear relationship between T₁ (in the presence of Gd(DTPA)^2-) and [GAG] over a large range of [GAG]. Furthermore, there was a strong agreement between the [GAG] calculated from [Gd(DTPA)^2-] and the actual [GAG] determined from the validated methods of calculations from [Na⁺] and the biochemical DMMB assay. Spatial distributions of GAG were easily observed in T₁-weighted and T₁-calculated MRI studies of intact human joints, with good histological correlation. Furthermore, in vivo clinical images of T₁ in the presence of Gd(DTPA)^2- (i.e., GAG distribution) correlated well with the validated ex vivo results after total knee replacement surgery, showing that it is feasible to monitor GAG distribution in vivo. This approach gives us the opportunity to image directly the concentration of GAG, a major and critically important macromolecule in human cartilage.

A schematic illustration of the
structure of cartilage.

The method is based on Donnan equilibrium, which Russ Hobbie and I describe in Section 9.1 of Intermediate Physics for Medicine and Biology. Assume the cartilage tissue (t) is bathed by saline (b). We will ignore all ions except the sodium cation, the chloride anion, and the negatively charged glycosaminoglycan (GAG). Cartilage is not enclosed by a semipermeable membrane, as analyzed in IPMB. Instead, the GAG molecules are fixed and immobile, so they act as if they cannot cross a membrane surrounding the tissue. Both the tissue and bath are electrically neutral, so [Na⁺]_b = [Cl^-]_b and [Na⁺]_t = [Cl^-]_t + [GAG^-], where we assume GAG is singly charged (we could instead just interpret [GAG^-] as being the fixed charge density). At the cartilage surface, sodium and chloride are distributed by a Boltzmann factor: [Na⁺]_t/[Na⁺]_b = [Cl^-]_b/[Cl^-]_t = exp(-eV/kT), where V is the electrical potential of the tissue relative to the bath, e is the elementary charge, k is the Boltzmann constant, and T is the absolute temperature. We can solve these equations for [GAG^-] in terms of the sodium concentrations: [GAG^-] = [Na⁺]_b ( [Na⁺]_t/[Na⁺]_b - [Na⁺]_b/[Na⁺]_t ).

Now, suppose you add a small amount of gadolinium diethylene triamine pentaacetic acid (Gd-DTPA^2-); so little that you can ignore it in the equations of neutrality above. The concentrations of Gd-DTPA on the two sides of the articular surface are related by the Boltzmann factor [Gd-DTPA^2-]_b/[Gd-DTPA^2-]_t = exp(-2eV/kT) [note the factor of two in the exponent reflecting the valance -2 of Gd-DTPA], implying that [Gd-DTPA^2-]_b/[Gd-DTPA^2-]_t = ( [Na⁺]_t/[Na⁺]_b )². Therefore,

We can determine [GAG^-] by measuring the sodium concentration in the bath and the Gd-DTPA concentration in the bath and the tissue. Section 18.6 of IPMB describes how gadolinium shortens the T₁ time constant of a magnetic resonance signal, so using T₁-weighted magnetic resonance imaging you can determine the gadolinium concentration in both the bath and the tissue.

From my perspective, I like dGEMRIC because it takes two seemingly disparate parts of IPMB, the section of Donnan equilibrium and the section on how relaxation times affect magnetic resonance imaging, and combines them to create an innovative imaging method. Bashir et al.’s paper is eloquent, so I will close this blog post with their own words.

The results of this study have demonstrated that human cartilage GAG concentration can be measured and quantified in vitro in normal and degenerated tissue using magnetic resonance spectroscopy in the presence of the ionic contrast agent Gd(DTPA)^2- … These spectroscopic studies therefore demonstrate the quantitative correspondence between tissue T₁ in the presence of Gd(DTPA)^2- and [GAG] in human cartilage. Applying the same principle in an imaging mode to obtain T₁ measured on a spatially localized basis (i.e., T₁-calculated images), spatial variations in [GAG] were visualized and quantified in excised intact samples…

In summary, the data presented here demonstrate the validity of the method for imaging GAG concentration in human cartilage… We now have a unique opportunity to study developmental and degenerative disease processes in cartilage and monitor the efficacy of medical and surgical therapeutic measures, for ultimately achieving a greater understanding of cartilage physiology in health and disease.

The Nuts and Bolts of Life: Willem Kolff and the Invention of the Kidney Machine

The Nuts and Bolts of Life:
Willem Kolff and the
Invention of the Kidney Machine,
by Paul Heiney.

In Chapter 5 of Intermediate Physics for Medicine and Biology, Russ Hobbie and I discuss the artificial kidney.

Two compartments, the body fluid and the dialysis fluid, are separated by a membrane that is porous to the small molecules to be removed and impermeable to larger molecules. If such a configuration is maintained long enough, then the concentration of any solute that can pass through the membrane will become the same on both sides.

The history of the artificial kidney is fascinating. Paul Heiney describes this story in his book The Nuts and Bolts of Life: Willem Kolff and the Invention of the Kidney Machine.

Willem Kolff…has battled to mend broken bodies by bringing mechanical solutions to medical problems. He built the first ever artificial kidney and a working artificial heart, and helped create the artificial eye. He s the true founder of the bionic age in which all human parts will be replaceable.

Heiney’s book is not a scholarly treatise and there is little physics in it, but Kolff’s personal story is captivating. Much of the work to develop the artificial kidney was done during World War II, when Kolff’s homeland, the Netherlands, was occupied by the Nazis. Kolff managed to create the first artificial organ while simultaneously caring for his patients, collaborating with the Dutch resistance, and raising five children. Kolff was a tinkerer in the best sense of the word, and his eccentric personality reminds me of the inventor of the implantable pacemaker, Wilson Greatbatch.

Below are some excepts from the first chapter of The Nuts and Bolts of Life. To learn more about Kolff, see his New York Times obituary.

What might a casual visitor have imagined was happening behind the closed door of Room 12a on the first floor of Kampen Hospital in a remote and rural corner of Holland on the night of 11 September 1945? There was little to suggest a small miracle was taking place; in fact, the sounds that emerged from that room could easily have been mistaken for an organized assault.

The sounds themselves were certainly sinister. There was a rumbling that echoed along the tiled corridors of the small hospital and kept patients on the floor below from their sleep; and the sound of what might be a paddle-steamer thrashing through water. All very curious…

The 67-year-old patient lying in Room 12a would have been oblivious to all this. During the previous week she had suffered high fever, jaundice, inflammation of the gall bladder and kidney failure. Not quite comatose, she could just about respond to shouts or the deliberative infliction of pain. Her skin was pale yellow and the tiny amount of urine she produced was dark brown and cloudy….

Before she was wheeled into Room 12a of Kampen Hospital that night, Sofia Schafstadt’s death was a foregone conclusion. There was no cure for her suffering; her kidneys were failing to cleanse her body of the waste it created in the chemical processes of keeping her alive. She was sinking into a body awash in her own poisons….

But that night was to be like no other night in medical history. The young doctor, Willem Kolff, then aged thirty-four and an internist at Kampen Hospital, brought to a great crescendo his work of much of the previous five years. That night, he connected Sofia Schafstadt to his artificial kidney – a machine born out of his own ingenuity. With it, he believed, for the first time ever he could replicate the function of one of the vital organs with a machine working outside the body…

The machine itself was the size of a sideboard and stood by the patient’s bed. The iron frame carried a large enamel tank containing fluid. Inside this rotated a drum around which was wrapped the unlikely sausage skin through which the patient’s blood flowed. And that, in essence, was it: a machine that could undoubtedly be called a contraption was about to become the world’s first successful artificial kidney…

John David Jackson (1925-2016)

Classical Electrodynamics, 3rd Ed,
by John David Jackson.

John David Jackson died on May 20 of this year. I am familiar with Jackson mainly through his book Classical Electrodynamics. Russ Hobbie and I cite Jackson in Chapter 14 of Intermediate Physics for Medicine and Biology.

The classical analog of Compton scattering is Thomson scattering of an electromagnetic wave by a free electron. The electron experiences the electric field E of an incident plane electromagnetic wave and therefore has an acceleration −eE/m. Accelerated charges radiate electromagnetic waves, and the energy radiated in different directions can be calculated, giving Eqs. 15.17 and 15.19. (See, for example, Jackson 1999, Chap. 14.) In the classical limit of low photon energies and momenta, the energy of the recoil electron is negligible.

Classical Electrodynamics, 2nd Ed,
by John David Jackson.

Classical Electrodynamics is usually known simply as “Jackson.” It is one of the top graduate textbooks in electricity and magnetism. When I was a graduate student at Vanderbilt University, I took an electricity and magnetism class based on the second edition of Jackson (the edition with the red cover). My copy of the 2nd edition is so worn that I have its spine held together by tape. Here at Oakland University I have taught from Jackson’s third edition (the blue cover). I remember my shock when I discovered Jackson had adopted SI units in the 3rd edition. He writes in the preface

My tardy adoption of the universally accepted SI system is a recognition that almost all undergraduate physics texts, as well as engineering books at all levels, employ SI units throughout. For many years Ed Purcell and I had a pact to support each other in the use of Gaussian units. Now I have betrayed him!

Classical Electrodynamics,
by John David Jackson.

Jackson has been my primary reference when I need to solve problems in electricity and magnetism. For instance, I consider my calculation of the magnetic field of a single axon to be little more than a classic “Jackson problem.” Jackson is famous for solving complicated electricity and magnetism problems using the tools of mathematical physics. In Chapter 2 he uses the method of images to calculate the the force between a point charge q and a nearby conducting sphere having the same charge q distributed over its surface. When the distance between the charge and the sphere is large compared to the sphere radius, the repelling force is given by Coulombs law. When the distance is small, however, the charge induces a surface charge of opposite sign on the sphere near it, resulting in an attractive force. Later in Chapter 2, Jackson uses Fourier analysis to calculate the potential inside a two-dimension slot having a voltage V on the bottom surface and grounded on the sides. He finds a series solution, which I think I could have done myself, but then he springs an amazing trick with complex variables in order to sum the series and get an entirely nonintuitive analytical solution involving an inverse tangent of a sine divided by a hyperbolic sine. How lovely.

My favorite is Chapter 3, where Jackson solves Laplace’s equation in spherical and cylindrical coordinate systems. Nerve axons and strands of cardiac muscle are generally cylindrical, so I am a big user of his cylindrical solution based on Bessel functions and Fourier series. Many of my early papers were variations on the theme of solving Laplace’s equation in cylindrical coordinates. In Chapter 5, Jackson analyzes a spherical shell of ferromagnetic material, which is an excellent model for a magnetic shield used in biomagnetic studies.

I have spent most of my career applying what I learned in Jackson to problems in medicine and biology.

Data Reduction and Error Analysis for the Physical Sciences

Data Reduction and Error Analysis
for the Physical Sciences,
by Philip Bevington and Keith Robinson.

In Chapter 11 of Intermediate Physics for Medicine and Biology, Russ Hobbie and I cite the book Data Reduction and Error Analysis for the Physical Sciences, by Philip Bevington and Keith Robinson.

The problem [of fitting a function to data] can be solved using the technique of nonlinear least squares…The most common [algorithm] is called the Levenberg-Marquardt method (see Bevington and Robinson 2003 or Press et al. 1992).

I have written about the excellent book Numerical Recipes by Press et al. previously in this blog. I was not too familiar with the book by Bevington and Robinson, so last week I checked out a copy from the Oakland University library (the second edition, 1992).

I like it. The book is a great resource for many of the topics Russ and I discuss in IPMB. I am not an experimentalist, but I did experiments in graduate school, and I have great respect for the challenges faced when working in the laboratory.

Their Chapter 1 begins by distinguishing between systematic and random errors. Bevington and Robinson illustrate the difference between accuracy and precision using a figure like this one:

a) Precise but inaccurate data. b) Accurate but imprecise data.

Next, they present a common sense discussion about significant figures, a topic that my students often don’t understand. (I assign them a homework problem with all the input data to two significant figures, and they turn in an answer--mindlessly copied from their calculator--containing 12 significant figures.)

In Chapter 2 of Data Reduction and Error Analysis, Bevington and Robinson introduce probability distributions.

Of the many probability distributions that are involved in the analysis of experimental data, three play a fundamental role: the binomial distribution [Appendix H in IPMB], the Poisson distribution [Appendix J], and the Gaussian distribution [Appendix I]. Of these, the Gaussian or normal error distribution is undoubtedly the most important in statistical analysis of data. Practically, it is useful because it seems to describe the distribution of random observations for many experiments, as well as describing the distributions obtained when we try to estimate the parameters of most other probability distributions.

Here is something I didn’t realize about the Poisson distribution:

The Poisson distribution, like the bidomial distribution, is a discrete distribution. That is, it is defined only at integral values of the variable x, although the parameter μ [the mean] is a positive, real number.

Figure J.1 of IPMB plots the Poisson distribution P(x) as a continuous function. I guess the plot should have been a histogram.

Chapter 3 addresses error analysis and propagation of error. Suppose you measure two quantities, x and y, each with an associated standard deviation σ_x and σ_y. Then you calculate a third quantity z(x,y). If x and y are uncorrelated, then the error propagation equation is

For instance, Eq. 1.40 in IPMB gives the flow of a fluid through a pipe, i, as a function of the viscosity of the fluid, η, and the radius of the pipe, R_p

The error propagation equation (and some algebra) gives the standard deviation of the flow in terms of the standard deviation of the viscosity and the standard deviation of the radius

When you have a variable raised to the fourth power, such as the pipe radius in the equation for flow, it contributes four times more to the flow’s percentage uncertainty than a variable such as the viscosity. A ten percent uncertainty in the radius contributes a forty percent uncertainty to the flow. This is a crucial concept to remember when performing experiments.

Bevington and Robinson derive the method of least squares in Chapter 4, covering much of the same ground as in Chapter 11 of IPMB. I particularly like the section titled A Warning About Statistics.

Equation (4.12) [relating the standard deviation of the mean to the standard deviation and the number of trails] might suggest that the error in the mean of a set of measurements x_i can be reduced indefinitely by repeated measurements of x_i. We should be aware of the limitations of this equation before assuming that an experimental result can be improved to any desired degree of accuracy if we are willing to do enough work. There are three main limitations to consider, those of available time and resources, those imposed by systematic errors, and those imposed by nonstatistical fluctuations.

Russ and I mention Monte Carlo techniques—the topic of Chapter 5 in Data Reduction and Error Analysis—a couple times in IPMB. Then Bevington and Robinson show how to use least squares to fit to various functions: a line (Chapter 6), a polynomial (Chapter 7), and an arbitrary function (Chapter 8). In Chapter 8 the Marquardt method is introduced. Deriving this algorithm is too involved for this blog post, but Bevington and Robinson explain all the gory details. They also provide much insight about the method, such as in the section Comments on the Fits:

Although the Marquardt method is the most complex of the four fitting routines, it is also the clear winner for finding fits most directly and efficiently. It has the strong advantage of being reasonably insensitive of the starting values of the parameters, although in the peak-over-background example in Chapter 9, it does have difficulty when the starting parameters of the function for the peak are outside reasonable ranges. The Marquardt method also has the advantage over the grid- and gradient-search methods of providing an estimate of the full error matrix and better calculation of the diagonal errors.

The rest of the book covers more technical issues that are not particularly relevant to IPMB. The appendix contains several computer programs written in Pascal. The OU library copy also contains a 5 1/2 inch floppy disk, which would have been useful 25 years ago but now is quaint.

Philip Bevington wrote the first edition of Data Reduction and Error Analysis in 1969, and it has become a classic. For many years he was a professor of physics at Case Western University, and died in 1980 at the young age of 47. A third edition was published in 2002. Download it here.

Rall's Equivalent Cylinder

Chapter 6 of Intermediate Physics for Medicine and Biology discusses nerve electrophysiology. In particular, Russ Hobbie and I derive the cable equation. This equation works great for a peripheral nerve with its single long cylindrical axon. In the brain, however, nerves end in branching networks of dendrites (see one of the famous drawings by Ramón y Cajal below). What equation describes the dendrites?

A drawing of a dendritic tree,
by Ramón y Cajal.

Wilfrid Rall answered this question by representing the dendrites as a branching network of fibers: the Rall model (Annals of the New York Academy of Sciences, Volume 96, Pages 1071–1092, 1962). Below I’
--> -->ll rederive the Rall model using the notation of IPMB. But—as I know some of you do not enjoy mathematics as much as I do—let me first describe his result qualitatively. Rall found that as you move along the dendritic tree, the fiber radius a gets smaller and smaller, but the number of fibers n gets larger and larger. Under one special condition, when na^3/2 is constant, the voltage along the dendrites obeys THE SAME cable equation that governs a single axon. This only works if distance is measured in length constants instead of millimeters, and time in time constants instead of milliseconds. Dendritic networks don't always have na^3/2 constant, but it is not a bad approximation, and provides valuable insight into how dendrites behave.
But instead of me explaining Rall’s goals, why not let Rall do so himself.

In this paper, I propose to focus attention upon the branching dendritic trees that are characteristic of many neurons, and to consider the contribution such dendritic trees can be expected to make to the physiological properties of a whole neuron. More specifically, I shall present a mathematical theory relevant to the question: How does a neuron integrate various distributions of synaptic excitation and inhibition delivered to its soma-dendritic surface. A mathematical theory of such integration is needed to help fill a gap that exists between the mathematical theory of nerve membrane properties, on the one hand, and the mathematical theory of nerve nets and of populations of interacting neurons, on the other hand.

I had the pleasure of knowing Rall when we both worked at the National Institutes of Health in the 1990s. He was trained as a physicist, and obtained his PhD from Yale. During World War II he worked on the Manhattan Project. He spent most of his career at NIH, and was a leader among scientists studying the theoretical electrophysiology of dendrites.

Rall receiving the Swartz Prize.

Now the math. First, let me review the cable model for a single axon, and then we will generalize the result to a network. The current i_i along an axon is related to the potential v and the resistance per unit length r_i by a form of Ohm's law

(Eq. 6.48 in IPMB). If the current changes along the axon, it must enter or leave through the membrane, resulting in an equation of continuity

(Eq. 6.49), where g_m is the membrane conductance per unit area and c_m is the membrane capacitance per unit area. Putting these two equations together and rearranging gives the cable equation

The axon length constant is defined as

and the time constant as

so the cable equation becomes

If we measure distance and time using the dimensionless variables X = x/λ and T = t/τ, the cable equation simplifies further to

Now, let’s see how Rall generalized this to a branching network. Instead of having one fiber, assume you have a variable number that depends on position along the network, n(x). Furthermore, assume the radius of each individual fiber varies, a(x). The cable equation can be derived as before, but because r_i now varies with position (r_i = 1/nπa²σ, where σ is the intracellular conductivity), we pick up an extra term

When I first looked at this equation, I thought “Aha! If r_i is independent of x, the new term disappears and you get the plain old cable equation.” It’s not quite that simple; λ also depends on position, so even without the extra term this is not the cable equation. Remember, we want to measure distance in the dimensionless variable X = x/λ, but λ depends on position, so the relationship between derivatives of x and derivatives of X is complicated

In terms of the dimensionless variables X and T, the cable equation becomes

If λr_i is constant along the axon, the ugly new term vanishes and you have the traditional cable equation. If you go back to the definition of r_i and λ in terms of a and n, you find that this condition is equivalent to saying that na^3/2 is constant along the network. If one fiber branches into two, the daughter fibers must each have a radius of 0.63 times the parent fiber radius. Dendritic trees that branch in this way act like a single fiber. This is Rall’s result: the Rall equivalent cylinder.

If you want to learn more about Rall’s work, read the book The Theoretical Foundation of Dendritic Function: Selected Papers of Wilfrid Rall with Commentaries, edited by Idan Segev, John Rinzel, and Gordon M. Shepherd. The foreword, by Terrence J. Sejnowski, says

The exploration of the electrical properties of dendrites by Wilfrid Rall provided many key insights into the computational resources of the neurons. Many of the papers in this collection are classics: dendrodendritic interactions in the olfactory bulb; nonlinear synaptic integration in motoneuron dendrites; active currents in pyramidal neuron apical dendrites. In each of these studies, insights arose from a conceptual leap, astute simplifying assumptions, and rigorous analysis. Looking back, one is impressed with the foresight shown by Rall in his choice of problems, with the elegance of his methods in attacking them, and with the impact that his conclusions have had for our current thinking. These papers deserve careful reading and rereading, for there are additional lessons in each of them that will reward the careful reader....It would be difficult to imagine the field of computational neuroscience today without the conceptual framework established over the last thirty years by Wil Rall, and for this we all owe him a great debt of gratitude.

Magneto-Aerotactic Bacteria Deliver Drug-Containing Nanoliposomes to Tumour Hypoxic Regions

In Chapter 8 of Intermediate Physics for Medicine and Biology, Russ Hobbie and I describe magnetotactic bacteria.

Several species of bacteria contain linear strings of up to 20 particles of magnetite, each about 50 nm on a side encased in a membrane (Frankelet al. 1979; Moskowitz 1995). Over a dozen different bacteria have been identified that synthesize these intracellular, membrane-bound particles or magnetosomes (Fig. 8.25). In the laboratory the bacteria align themselves with the local magnetic field. In the problems you will learn that there is sufficient magnetic material in each bacterium to align it with the earth’s field just like a compass needle. Because of the tilt of the earth’s field, bacteria in the wild can thereby distinguish up from down.

Other bacteria that live in oxygen-poor, sulfide-rich environments contain magnetosomes composed of greigite (Fe₃S₄), rather than magnetite (Fe₃O₄). In aquatic habitats, high concentrations of both kinds of magnetotactic bacteria are usually found near the oxic–anoxic transition zone (OATZ). In freshwater environments the OATZ is usually at the sediment–water interface. In marine environments it is displaced up into the water column. Since some bacteria prefer more oxygen and others prefer less, and they both have the same kind of propulsion and orientation mechanism, one wonders why one kind of bacterium is not swimming out of the environment favorable to it. Frankel and Bazylinski(1994) proposed that the magnetic field and the magnetosomes keep the organism aligned with the field, and that they change the direction in which their flagellum rotates to move in the direction that leads them to a more favorable concentration of some desired chemical.

I enjoy learning about the biology and physics of magnetotactic bacteria, but I never expected that they had anything to do with medicine. Then last month a paper published in Nature Nanotechnology discussed using these bacteria to treat cancer!

Oxygen-depleted hypoxic regions in the tumour are generally resistant to therapies. Although nanocarriers have been used to deliver drugs, the targeting ratios have been very low. Here, we show that the magneto-aerotactic migration behaviour of magnetotactic bacteria, Magnetococcus marinus strain MC-1 (ref. 4), can be used to transport drug-loaded nanoliposomes into hypoxic regions of the tumour. In their natural environment, MC-1 cells, each containing a chain of magnetic iron-oxide nanocrystals, tend to swim along local magnetic field lines and towards low oxygen concentrations based on a two-state aerotactic sensing system. We show that when MC-1 cells bearing covalently bound drug-containing nanoliposomes were injected near the tumour in severe combined immunodeficient beige mice and magnetically guided, up to 55% of MC-1 cells penetrated into hypoxic regions of HCT116 colorectal xenografts. Approximately 70 drug-loaded nanoliposomes were attached to each MC-1 cell. Our results suggest that harnessing swarms of microorganisms exhibiting magneto-aerotactic behaviour can significantly improve the therapeutic index of various nanocarriers in tumour hypoxic regions.

The IOP website physicsworld.com published an article by Belle Dumé describing this study. It begins

Bacteria that respond to magnetic fields and low oxygen levels may soon join the fight against cancer. Researchers in Canada have done experiments that show how magneto-aerotactic bacteria can be used to deliver drugs to hard-to-reach parts of tumours. With further development, the method could be used to treat a variety of solid tumours, which account for roughly 85% of all cancers.

A similar article, also by Dumé, can be found on medicalphysicsweb.com

As cancer cells proliferate, they consume large amounts of oxygen. This results in oxygen-poor regions in a tumour. It is notoriously difficult to treat these hypoxic regions using conventional pharmaceutical nanocarriers, such as liposomes, micelles and polymeric nanoparticles.

Now, a team led by Sylvain Martel of the NanoRobotics Laboratory at the Polytechnique Montréal has developed a method that exploits the magnetotactic bacteria Magnetoccus marinus (MC-1) to overcome this problem.

Pretty cool stuff.

Rutherford Scattering and the Differential Cross Section

In Chapter 14 of Intermediate Physics for Medicine and Biology, Russ Hobbie and I discuss the differential cross section.

We may wish to know the probability that particles…are scattered in a certain direction. We have to consider the probability that they are scattered into a small solid angle dΩ. In this case, σ is called the differential scattering cross section and is often written as

The units of the differential scattering cross section are m² sr^-1. The differential cross section depends on θ, the angle between the directions of travel of the incident and scattered particles.

Perhaps the most famous differential cross section is the Rutherford scattering formula. Ernest Rutherford (who I have discussed before in this blog) derived this formula to explain the results of his alpha particle scattering experiments, in which he fired alpha particles at a thin metal foil and determined the angle of scattering by observing the light produced when a scattered particle hit a zinc sulfide screen. His formula assumes a nonrelativistic alpha particle scatters off a massive (no recoil), spinless, bare, positively charged target nucleus. Below is a new homework problem providing some practice with the Rutherford formula

Problem 16 ½. An example of a differential cross section is the Rutherford scattering formula

(a) Plot dσ/dΩ versus θ over the range 0 to π.

(b) Repeat part (a) using semilog graph paper.

(c) The constant A is equal to

where q and Q are the charges of the alpha particle and nucleus, and E is the alpha particle energy. Show that A has the units of m² sr^-1. Hint: steradians, like radians, are dimensionless (see Appendix A).

(d) Interpret what happens physically when θ is π. What is the value of the cosecant of π/2? Write A in terms of the distance of closest approach of an alpha particle to the nucleus. Hint: see Chapter 17, Problem 2.

(e) Note that dσ/dΩ goes to infinity as θ goes to zero. Interpret this result physically. What assumption did Rutherford make that may be responsible for this unphysical behavior?

(f) Integrate dσ/dΩ over θ from 0 to π. You may need to use a good table of integrals. Explain your result (which may surprise you) physically.

The Making of the Atomic Bomb,
by Richard Rhodes.

Here is the history of the Rutherford scattering experiment, as told by Richard Rhodes in The Making of the Atomic Bomb.

[Hans] Geiger [Rutherford’s assistant] went to work on alpha scattering, aided by Ernest Marsden, then an eighteen-year-old Manchester undergraduate. They observed alpha particles coming out of a firing tube and passing through foils of such metals as aluminum, silver, gold, and platinum. The results were generally consistent with expectation: alpha particles might very well accumulate as much as two degrees of total deflection bouncing around among atoms of the plum-pudding sort [an early model of atomic structure proposed by J. J. Thomson]. But the experiment was troubled with stray particles. Geiger and Marsden thought molecules in the walls of the firing tube might be scattering them. They tried eliminating the strays by narrowing and defining the end of the firing tube with a series of graduated metal washers. That proved no help.

Rutherford wandered into the room. The three men talked over the problem. Something about it alerted Rutherford’s intuition for promising side effects. Almost as an afterthought he turned to Marsden and said, “See if you can get some effect of alpha particles directly reflected from a metal surface.” Marsden knew that a negative result was expected—alpha particles shot through thin foils, they did not bounce back form them—but that missing a positive result would be an unforgivable sin. He took great care to prepare a strong alpha source. He aimed the pencil-narrow beam of alphas at a forty-five degree angle onto a sheet of gold foil. He positioned his scintillation screen on the same side of the foil, beside the alpha beam, so that a particle bouncing back would strike the screen and register as a scintillation. Between firing tube and screen he interposed a thick lead plate so no direct alpha particles could interfere.

Immediately, and to his surprise, he found what he was looking for. “I remember well reporting the result to Rutherford,” he wrote, “…when I met him on the steps leading to his private room, and the joy with which I told him…”

Rutherford had been genuinely astonished by Marsden’s results. “It was quite the most incredible event that has ever happened to me in my life,” he said later. “It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you. On consideration I realized that this scattering backwards must be the result of a single collision, and when I made calculations I saw that it was impossible to get anything of that order of magnitude unless you took a system in which the greatest part of the mass of the atom was concentrated in a minute nucleus.”

The Biomechanics of Solids and Fluids: The Physics of Life

“The Biomechanics of Solids and Fluids:
The Physics of Life,”
by David Alexander.

This summer a review article about biomechanics by David Alexander appeared in the European Journal of Physics: “The Biomechanics of Solids and Fluids: The Physics of Life” (Volume 37, Article 053011, 2016). It serves as an excellent supplement for much of the material in Chapter 1 (Mechanics) in Intermediate Physics for Medicine and Biology. It describes the biomechanics of solids (elasticity) and fluids (fluid mechanics).

Biomechanics borrows and extends engineering techniques to study the mechanical properties of organisms and their environments. Like physicists and engineers, biomechanics researchers tend to specialize on either fluids or solids (but some do both). For solid materials, the stress–strain curve reveals such useful information as various moduli, ultimate strength, extensibility, and work of fracture. Few biological materials are linearly elastic so modified elastic moduli are defined. Although biological materials tend to be less stiff than engineered materials, biomaterials tend to be tougher due to their anisotropy and high extensibility. Biological beams are usually hollow cylinders; particularly in plants, beams and columns tend to have high twist-to-bend ratios. Air and water are the dominant biological fluids. Fluids generate both viscous and pressure drag (normalized as drag coefficients) and the Reynolds number (Re) gives their relative importance. The no-slip conditions leads to velocity gradients (‘boundary layers’) on surfaces and parabolic flow profiles in tubes. Rather than rigidly resisting drag in external flows, many plants and sessile animals reconfigure to reduce drag as speed increases. Living in velocity gradients can be beneficial for attachment but challenging for capturing particulate food. Lift produced by airfoils and hydrofoils is used to produce thrust by all flying animals and many swimming ones, and is usually optimal at higher Re. At low Re, most swimmers use drag-based mechanisms. A few swimmers use jetting for rapid escape despite its energetic inefficiency. At low Re, suspension feeding depends on mechanisms other than direct sieving because thick boundary layers reduce effective porosity. Most biomaterials exhibit a combination of solid and fluid properties, i.e., viscoelasticity. Even rigid biomaterials exhibit creep over many days, whereas pliant biomaterials may exhibit creep over hours or minutes. Instead of rigid materials, many organisms use tensile fibers wound around pressurized cavities (hydrostats) for rigid support; the winding angle of helical fibers greatly affects hydrostat properties. Biomechanics researchers have gone beyond borrowing from engineers and adopted or developed a variety of new approaches—e.g., laser speckle interferometry, optical correlation, and computer-driven physical models—that are better-suited to biological situations.

One of my favorite parts of the review are the references. Alexander cites many of his own publications, including his book Nature’s Flyers: Birds, Insects, and the Biomechanics of Flight. For some reason, he didn’t cite his recent book On the Wing: Insects, Pterosaurs, Birds, Bats and the Evolution of Animal Flight. By the way, David Alexander is not the same as R. McNeill Alexander, who published Principles of Animal Locomotion, which is also cited in the review, and who died earlier this year. The review cites several works by Mark Denny, although not my favorite: Air and Water. Alexander cites over a dozen works by Steven Vogel, whose Life in Moving Fluids appears on my ideal bookshelf. Finally, he writes that “James Gordon’s book Structures, or Why Things Don’t Fall Down (Gordon 1978) is one of the most entertaining and readable introductions to a technical topic ever written.” I read Gordon’s book many years ago and had almost forgotten it. Alexander is right, it’s a gem.

In Figure 1.21, Russ Hobbie and I show a typical stress-strain curve. Alexander shows similar curves, and analyzes them in more detail. Like our book, he develops the concepts of Young’s modulus, shear modulus, strength, and Poisson’s ratio. Alexander introduces another concept: the strain energy density, which is the area under the stress-strain curve. Stress has units of N/m², and strain is dimensionless, so the strain energy density has units of N/m² = J/m³. Alexander writes “this key value measures how much work a material absorbs before breaking, and is sometimes referred to as ‘toughness’. Perhaps counterintuitively, some very hard, rigid materials are not very tough, whereas many floppy, easily extended materials are very tough.”

The section on fluid dynamics covers much of the same ground as analyzed in IPMB. It also discusses high Reynold’s number flow, including turbulence, flow separation, boundary layers, lift, and drag. These are fascinating topics, and are vital for understanding animal flight, but do not impact the low Reynold’s number flow that Russ and I focus on.

One topic that Russ and I give a brief mention is viscoelasticity. Alexander spends more time on this interesting subject.

Most biological materials do not fit perfectly into the solid or fluid categories as engineers and physicists have usually defined them. Many biological structures that we would ordinarily consider solid actually have a time-dependent response to loading that gives them a partly fluid character. A proper Hookean material behaves the same way whether it is loaded for a second or a week: remove the load and it returns to its original shape. A viscoelastic solid, however, displays a property called creep : apply a load briefly and the material will spring back just as if it were Hookean. Apply the same load for a prolonged period, however, and the material will continue to deform gradually. When the load is removed, the material may have acquired a permanent deformation, and if so, the longer it is loaded, the greater the permanent deformation.

Alexandar’s review is a great place to go for more about biomechanics after reading Chapter 1 of IPMB. I highly recommend it.

Whiplash

Last week, my wife Shirley and I were in an automobile accident. We suffered no serious injuries, thank you, but the car was totaled and we were sore for several days. After the obligatory reflections on the meaning of life, I began to think critically about the biomechanics of auto accident injuries.

Our car was at a complete stop, and the idiot in the other car hit us from behind. The driver’s side air bag deployed and the impact pushed us off to the right of the road (we hit the car in front of us in the process), while the idiot’s car ended up on the opposite shoulder. It looked a little like this; we were m₂ and the idiot was m₁:

The collision dynamics of our car accident.

The police came and our poor car was carried off on a wrecker to a junk yard. Shirley and I walked home; the accident occurred about a quarter mile from our house.

My neck is still stiff. Presumably I suffered a classic—but not too severe—whiplash. Although Intermediate Physics for Medicine and Biology does not discuss whiplash, it does cover most of the concepts needed to understand it: acceleration, shear forces, torques, and biomechanics. Paul Davidovits describes whiplash briefly in Physics in Biology and Medicine. From the second edition:

5.7  Whiplash Injury

Neck bones are rather delicate and can be fractured by even a moderate force. Fortunately the neck muscles are relatively strong and are capable of absorbing a considerable amount of energy. If, however, the impact is sudden, as in a rear-end collision, the body is accelerated in the forward direction by the back of the seat,  and the unsupported neck is then suddenly yanked back at full speed. Here the muscles do not respond fast enough and all the energy is absorbed by the neck bones, causing the well-known whiplash injury.

You can learn more about the physics of whiplash in the paper “Kinematics of a Head-Neck Model Simulating Whiplash” published in The Physics Teacher (Volume 46, Pages 88–91, 2008).

In a typical rear-end collision, the vehicle accelerates forward when struck and the torso is pushed forward by the seat. The structural response of the cervical spine is dependent upon the acceleration-time pulse applied to the thoracic spine and interaction of the head and spinal components. During the initial phases of the impact, it is obvious that the lower cervical vertebrae move horizontally faster than the upper ones. The shear force is transmitted from the lower cervical vertebrae to the upper ones through soft tissues between adjacent vertebrae one level at a time. This shearing motion contributes to the initial development of an S-shape curvature of the neck (the upper cervical spine undergoes flexion while the lower part undergoes extension), which progresses to a C-shape curvature. At the end of the loading phase, the entire head-neck complex is under the extension mode with a single curvature. This implies the stretching of the anterior and compression of the posterior parts of the cervical spine.

Here are links to videos showing what happens to the upper spine during whiplash:

http://www.injuryresources.com/brain-injury/injury44.html

http://www.injuryresources.com/brain-injury/injury45.html

http://www.injuryresources.com/brain-injury/injury46.html

Injury from whiplash depends on the acceleration. What sort of acceleration did my head undergo? I don’t know the speed of the idiot’s car, but I will guess it was 25 miles per hour, which is equal to about 11 meters per second. Most of the literature I have read suggests that the acceleration resulting from such impacts occurs in about a tenth of a second. Acceleration is change in speed divided by change in time (see Appendix B in IPMB), so (11 m/s)/(0.1 s) = 110 m/s², which is about 11 times the acceleration of gravity, or 11 g. Yikes! Honestly, I don’t know the idiot’s speed. He may have been slowing down before he hit me, but I don’t recall any skidding noises just before impact.

What lesson do I take from this close call with death? My hero Isaac Asimov—who wrote over 500 books in his life—was asked what he would do if told he had only six months to live. His answer was “type faster.” Sounds like good advice to me!

Our car, after the accident.