Confocal Microscopy

Russ Hobbie and I don’t talk much about microscopy in Intermediate Physics for Medicine and Biology. In the homework problems to Chapter 14 (Atoms and Light) we describe the compound microscope, but that is about it. Physics, however, plays a big role in microscopy. In this post, I attempt to explain the physics behind the confocal microscope. I leave out much, but I hope this explanation conveys the essence of the technique.

Start with a simple converging lens. The lens is often indicated by a vertical line with triangles on the top and bottom, but this is shorthand for the dashed concave lens shown below. Assume this is the objective lens of your microscope. A lens has two focal points. Light originating at the left focal point exits the lens horizontally (yellow), like in a searchlight. Light coming from a distant object (purple) converges at the right focal point, like in a telescope.

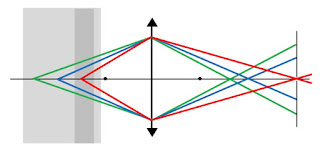
When an object is not so distant, the light converges at a point beyond the focal point; the closer the object, the farther back it converges. You can calculate the point where the light converges using the thin lens equation (Eq. 14.64 in IPMB). Below I show three rays originating at different positions in a sample of biological tissue. The colors (green, blue, and red) do not indicate different wavelengths of light; I use different colors so the rays are easier to follow. Light originating deep in the sample (green) converges just beyond the right focal point, but light originating near the front of the sample (red) converges far beyond the focal point. This is why in a camera you can adjust the focus by changing the distance from the lens to the detector.

Suppose you wanted to detect light from only the center of the sample. You could put an opaque screen containing a small pinhole beyond the focal point of the lens, just where the blue rays converge. All the light originating from the center of the sample would pass through the pinhole. The light from deep in the sample (green) would be out of focus, so most of this light would be blocked by the screen. Likewise, light from the front of the sample (red) is even more out of focus, and only a tiny bit passes through the pinhole. So, voilá, the light detected beyond the pinhole is almost entirely from the center of the sample.

Do you want to view a different depth? Just move the screen/pinhole to the right or left, and you can image shallower or deeper positions.

In this way, you build up an image of the sample as a function of depth.

How do you get information in the plane at one depth? In confocal microscopy, you usually scan a laser at different positions in the x,y plane (taking z as the distance from the lens). Pixel by pixel, you build up an image, then adjust the position of the screen and build up another image, and then another and another.

Often, confocal microscopy is used with samples that emit fluoresced light. You shine the narrow laser beam of short-wavelength light onto the sample from the left. The sample then emits long-wavelength light as molecules in the sample fluoresce. You can filter out the short-wavelength light, and just image the long-wavelength light. Biologists play all kinds of tricks with fluorescence, such as attaching a fluorescent molecule to the particular structure in the sample they want to image.

There are advantages and disadvantages of a confocal microscope. On advantage is that your detector, positioned to the right of the screen/pinhole, need not be an array like in a camera. A single detector is sufficient; you build up the spatial information by scanning the laser beam (x,y) and the pinhole (z) to obtain full three-dimensional information that you can then manipulate with a computer to create informative and beautiful pictures. One disadvantage is that you have to scan both the laser and the pinhole in synchrony, which is not easy. All this scanning takes time, although video-rate scans are possible using modern technology. Also, most of your fluoresced light gets blocked by the screen, so you need an intense light source that may bleach of your fluorescent tag.

The confocal microscope was invented by Marvin Minsky, who died last year after a productive career in science. Minsky was an undergraduate physics major who went on to study mathematics, computer science, artificial intelligence, robotics, and consciousness. Isaac Asimov claimed in his biography In Joy Still Felt that only two people he knew were more intelligent than he was: Carl Sagan and Minsky. Marvin Minsky and his confocal microscope illustrate the critical role of physics in medicine and biology.

Applying Magneto-Rheology to Reduce Blood Viscosity and Suppress Turbulence to Prevent Heart Attacks

Recently, Russ Hobbie pointed out to me an abstract presented at the 2017 American Physical Society March Meeting about “Applying Magneto-Rheology to Reduce Blood Viscosity and Suppress Turbulence to Prevent Heart Attacks," by Rongjia Tao.

Heart attacks are the leading causes of death in USA. Research indicates one common thread, high blood viscosity, linking all cardiovascular diseases. Turbulence in blood circulation makes different regions of the vasculature vulnerable to development of atherosclerotic plaque. Turbulence is also responsible for systolic ejection murmurs and places heavier workload on heart, a possible trigger of heart attacks. Presently, neither medicine nor method is available to suppress turbulence. The only method to reduce the blood viscosity is to take medicine, such as aspirin. However, using medicine to reduce the blood viscosity does not help suppressing turbulence. In fact, the turbulence gets worse as the Reynolds number goes up with the viscosity reduction by the medicine. Here we report our new discovery: application of a strong magnetic field to blood along its flow direction, red blood cells are polarized in the magnetic field and aggregated into short chains along the flow direction. The blood viscosity becomes anisotropic: Along the flow direction the viscosity is significantly reduced, but in the directions perpendicular to the flow the viscosity is considerably increased. In this way, the blood flow becomes laminar, turbulence is suppressed, the blood circulation is greatly improved, and the risk for heart attacks is reduced. While these effects are not permanent, they last for about 24 hours after one magnetic therapy treatment.

The report is related to an earlier paper by Tao and Ke Huang “Reducing Blood Viscosity with Magnetic Fields” (Phys Rev E, Volume 84, Article Number 011905, 2011). The APS published a news article about this work.

I have some concerns. Let’s use basic physics, like that discussed in Intermediate Physics for Medicine and Biology, to make order-of-magnitude estimates of the forces acting on a red blood cell.

First, we’ll estimate the dipole-dipole magnetic force. A red blood cell has a funny shape, but for our back-of-the-envelope calculations let’s consider it to be a cube 5 microns on a side. The magnetization M, the magnetic field intensity H, and the magnetic susceptibility χ_m are related by M = χ_m H (Eq. 8.31, all equation numbers from the 5th edition of IPMB), and H is related to the applied magnetic field B by B = μ_o H (Eq. 8.30), where μ_o is the permeability of free space. The total magnetic dipole of a red blood cell, m, is then a³M (Eq. 8.27), or m = a³χ_mB/μ_o. If we use χ_m = 10^-5, B = 1 T, and μ_o = 4π × 10^-7 T m/A, the dipole strength is about 10^-15 A m². The magnetic field produced by this magnetic dipole in an adjacent red blood cell is about μ_om/(4πa³) = 10^-6 T (Eq. 18.32). The force on a magnetic dipole in this nonuniform magnetic field is approximately mB/a = 2 × 10^-16 N (Eq. 8.26).

What other forces act on this red blood cell? Consider a cell in an arteriole that has a radius of 30 μm, is 10 mm long, and has a pressure drop from one end of the arteriole to the other of 45 torr = 6000 Pa (see Table 1.4 of IPMB). The pressure gradient dP/dx is therefore 6 × 10⁵ Pa/m. The pressure difference between one side of a red blood cell and the other should be the product of the pressure gradient and the cell length. The force is this pressure difference times the surface area, or a³dP/dx = 8 × 10^-11 N. This force is about 400,000 times larger than the magnetic force calculated above.

Another force arises from friction between the fluid and the cell. It is equal to the product of the surface area (a²), the viscosity η, and the velocity gradient (Eq. 1.33). Take the blood viscosity to be 3 × 10^-3 Pa s. If we assume Poiseuille flow, the average speed of the blood in the arteriole is 0.02 m/s (Eq. 1.37). The average velocity gradient should be the average speed divided by the radius, or about 700 1/s. The viscous force is then 5  × 10^-11 N. This is almost the same as the pressure force. (Had we done the calculation more accurately, we should have found the two forces have the same magnitude and cancel each other out, because the blood is not accelerating).

Another small force acting on the red blood cell is gravity. The gravitational force is the density times the volume times the acceleration of gravity (Eq. 1.31). If we assume a density of 1000 kg/m³, this force is equal to about 10^-12 N. Even if this overestimates the force of gravity by a factor of a thousand because of buoyancy, it is still nearly an order of magnitude larger than the magnetic force.

These back-of-the-envelope calculations suggest that the dipole-dipole force is very small compared to other forces acting on the red blood cell. It is not obvious how it could trigger cell aggregation.

Let me add a few other points.

• The abstract talks about suppressing turbulence. However, as Russ and I point out in IPMB, turbulence is only important in the largest vessels of the circulatory system, such as the aorta. In the vast majority of vessels there is no turbulence to suppress. 
• In their 2011 paper, Tao and Huang claim the change in viscosity is caused by aggregation of blood cells, and their Fig. 3c shows one such clump of about a dozen cells. However, capillaries are so small that blood cells go through them one at a time. Aggregates of cells might not be able to pass through a capillary. 
• If a magnetic field makes dramatic changes in blood viscosity, then you should experience noticeable changes in blood flow and blood pressure during magnetic resonance imaging, which can expose you to magnetic fields of several tesla. I have not seen any reports of such hemodynamic changes during an MRI. 
• I would expect that an aggregate of blood cells blocking a vessel could cause a stroke. I have never heard of an increased risk of stroke when a person is exposed to a magnetic field. 
• Tau and Huang claim that for the dipole interaction energy to be stronger than thermal energy, kT, the applied magnetic field should be on the order of 1 T. I have reproduced their calculation and they are correct, but I am not sure kT is the relevant energy for comparison. A 1 T magnetic field would result in a dipole-dipole interaction energy for the entire red blood cell of about kT. At the temperature of the human body kT is about 1/40 of an electron volt, which is less than the energy of one covalent bond. There are about 10¹⁴ atoms making up a red blood cell. Is one extra bond among those hundred million million atoms going to cause aggregation? 
• The change in viscosity apparently depends on direction. I can see how you could adjust the geometry so the magnetic field is parallel to the blood flow for one large artery or vein, but the arterioles, veinuoles, and especially capillaries are going to be oriented every which way. Blood flow is slower in these small vessels, so red blood cells spend a large fraction of their time in them. I expect that in some vessels the viscosity would go up, and in others it would go down. 
• Tao claims that the increase in viscosity lasts 24 hours after the magnetic field is turned off. If the dipole-dipole interaction causes this effect, why does it last so long after the magnetic field is gone? Perhaps the magnetic interaction pushes the cells together and then other chemical reactions cause them to stick to each other. But if that were the case, then why are the cells not sticking together whenever they bump into each other as they tumble through the circulatory system? 
• Finally--and this is a little out of my expertise so I am on shakier ground here--doctors recommend aspirin because of its effect on blot clotting, not because it reduces viscosity.

What lessons can we learn from this analysis? First, I am not convinced that this effect of magnetism on blood viscosity is real. I could be wrong, and I may be missing some key piece of the puzzle. I'm a simple man, and the process may be inherently complex. Nevertheless, it just doesn’t make sense to me. Second, you should always make back-of-the-envelope estimations of the effects you study. Russ and I encourage such estimates in Intermediate Physics for Medicine and Biology. Get into the habit of using order-of-magnitude calculations to check if your results are reasonable.

Free-Radical Chain Reactions that Spread Damage and Destruction

One way radiation damages tissue is by producing free radicals, also known as reactive oxygen species. In Chapter 16 of Intermediate Physics for Medicine and Biology, Russ Hobbie and I discuss these molecules:

High-LET [linear energy transfer] radiation produces so many ion pairs along its path that it exerts a direct action on the cellular DNA. Low-LET radiation can also ionize, but it usually acts indirectly. It ionizes water (primarily) according to the chemical reaction

H₂O → H₂O⁺ + e^- .

The H₂O⁺ ion decays with a lifetime of about 10^-10 s to the hydroxyl free radical:

H₂O⁺ + H₂O → H₃O⁺ + OH .

This then produces hydrogen peroxide and other free radicals that cause the damage by disrupting chemical bonds in the DNA.

Free radicals are produced not only by water, but also by oxygen, O₂. Tissues without much oxygen (such as the ischemic core of a tumor) are resistant to radiation damage.

Oxygen, by Nick Lane.

Nick Lane’s book Oxygen: The Molecule that Made the World explains how radiation interacts with tissue through free radicals. In his Chapter 6, “Treachery in the Air: Oxygen Poisoning and X-Irradiation: A Common Mechanism,” he writes:

A free radical is loosely defined as any molecule capable of independent existence that has an unpaired electron. This tends to be an unstable electronic configuration. An unstable molecule in search of stability is quick to react with other molecules. Many free radicals are, accordingly, very reactive…

The three intermediates formed by irradiating water, the hydroxyl radicals, hydrogen peroxide and superoxide radicals, react in very different ways. However, because all three are linked and can be formed from each other, they might be considered equally dangerous…

Hydroxyl radicals (^•OH) are the first to be formed. These are extremely reactive fragments, the molecular equivalents of random muggers. They can react with all biological molecules at speeds approaching their rate of diffusion. This means that they react with the first molecules in their path and it is virtually impossible to stop them from doing so. They cause damage even before leaving the barrel of the gun…

If radiation strips a second electron from water, the next fleeting intermediate is hydrogen peroxide (H₂O₂)…Hydrogen peroxide is unusual in that it lies chemically exactly half way between oxygen and water. This gives the molecule something of a split personality. Like a would-be reformed mugger, whose instinct is pitted against his judgement, it can go either way in its reactions….[A] dangerous and significant reaction, however, takes place in the presence of iron, which can pass electrons one at a time to hydrogen peroxide to generate free radicals. If dissolved iron is present, hydrogen peroxide is a real hazard…

The third of our intermediates … [is] the superoxide radical (O₂^•-). Like hydrogen peroxide, the superoxide radical is not terribly reactive. However, it too has an affinity for iron…

In summary, then, the three intermediates between water and oxygen operate as an insidious catalytic system that damages biological molecules in the presence of iron. Superoxide radicals release iron from storage depots and convert it into the soluble form. Hydrogen peroxide reacts with soluble iron to generate hydroxyl radicals. Hydroxyl radicals attack all proteins, lipids and DNA indiscriminately, initiating destructive free-redical chain reactions that spread damage and destruction.

I fear that physics and biology alone are not enough to understand how radiation interacts with tissue; we need some chemistry too.

Magnetic Force Microscopy for Nanoparticle Characterization

In Chapter 8 of Intermediate Physics for Medicine and Biology, Russ Hobbie and I discuss biomagnetism. The 5th edition of IPMB contains a brief new section on magnetic nanoparticles

8.8.4 Magnetic Nanoparticles

Small single-domain nanoparticles (10–70 nm in diameter) are used to treat cancer (Jordan et al. 1999; Pankhurst et al. 2009). The particles are injected into the body intravenously. Then an oscillating magnetic field is applied. It causes the particles to rotate, heating the surrounding tissue. Cancer cells are particularly sensitive to damage by hyperthermia. Often the surface of the nanoparticles can be coated with antibodies that cause the nanoparticle to be selectively taken up by the tumor, providing more localized heating of the cancer.

Suppose you wanted to image the distribution of nanoparticles in tissue. How would you do it? In IPMB we describe several ways to map magnetic field distributions, including using a superconducting quantum interference device (SQUID) magnetometer. Is there a way to get even better spatial resolution than using a SQUID? Gustavo Cordova, Brenda Yasie Lee, and Zoya Leonenko recently published a review in the NanoWorld Journal describing “Magnetic Force Microscopy for Nanoparticle Characterization” (Volume 2, Pages 10–14, 2016). Their abstract states

Since the invention of the atomic force microscope (AFM) in 1986, there has been a drive to apply this scanning probe technique or a form of this technique to various disciplines in nanoscale science. Magnetic force microscopy (MFM) is a member of a growing family of scanning probe methods and has been widely used for the study of magnetic materials. In MFM a magnetic probe is used to raster-scan the surface of the sample, of which its magnetic field interacts with the magnetic tip to offer insight into its magnetic properties. This review will focus on the use of MFM in relation to nanoparticle characterization, including superparamagnetic iron oxide nanoparticles, covering MFM imaging in air and in liquid environments.

Figure 1 from their paper shows how the MFM “two-pass technique” works: a first scan produces a topographical image using an atomic force microscope, and then a second pass creates a magnetic image using a magnetic force microscope. Both the AFM and MFM are based on using a small, nanometer sized scanning tip attached to a cantilever to detect small-scale tip deflections.

Their Figure 2 shows the results of MFM imaging of superparamagnetic iron oxide nanoparticles (SPIONs). The technique has sufficient sensitivity that they can measure how the size distribution of SPIONs depends on the particle coating.

Cordova et al. conclude

Considering rapid development of novel applications of magnetic nanoparticles in medicine and biomedical nanotechnology, as therapeutic agents, contrast agents in MRI imaging and drug delivery [3] MFM characterization of nanoparticles becomes more valuable and desirable. Overall, MFM has proven itself to be an effective yet underused tool that offers great potential for the localization and characterization of magnetic nanoparticles.

The magnetic force microscope does not have the exquisite picotesla sensitivity and millisecond time resolution of a SQUID, and it requires access to the tissue surface so you can scan over it. But for static, strong-field systems such as magnetic nanoparticle distributions, the magnetic force microscope provides exceptional spatial resolution, and represents one more tool in the physicists arsenal for imaging magnetic fields in biology.