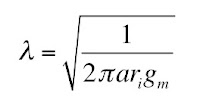|
| A drawing of a dendritic tree, by Ramón y Cajal. |
--> -->ll rederive the Rall model using the notation of IPMB. But—as I know some of you do not enjoy mathematics as much as I do—let me first describe his result qualitatively. Rall found that as you move along the dendritic tree, the fiber radius a gets smaller and smaller, but the number of fibers n gets larger and larger. Under one special condition, when na3/2 is constant, the voltage along the dendrites obeys THE SAME cable equation that governs a single axon. This only works if distance is measured in length constants instead of millimeters, and time in time constants instead of milliseconds. Dendritic networks don't always have na3/2 constant, but it is not a bad approximation, and provides valuable insight into how dendrites behave.
But instead of me explaining Rall’s goals, why not let Rall do so himself.
In this paper, I propose to focus attention upon the branching dendritic trees that are characteristic of many neurons, and to consider the contribution such dendritic trees can be expected to make to the physiological properties of a whole neuron. More specifically, I shall present a mathematical theory relevant to the question: How does a neuron integrate various distributions of synaptic excitation and inhibition delivered to its soma-dendritic surface. A mathematical theory of such integration is needed to help fill a gap that exists between the mathematical theory of nerve membrane properties, on the one hand, and the mathematical theory of nerve nets and of populations of interacting neurons, on the other hand.I had the pleasure of knowing Rall when we both worked at the National Institutes of Health in the 1990s. He was trained as a physicist, and obtained his PhD from Yale. During World War II he worked on the Manhattan Project. He spent most of his career at NIH, and was a leader among scientists studying the theoretical electrophysiology of dendrites.
Rall receiving the Swartz Prize.
(Eq. 6.49), where gm is the membrane conductance per unit area and cm is the membrane capacitance per unit area. Putting these two equations together and rearranging gives the cable equation
The axon length constant is defined as
and the time constant as
so the cable equation becomes
If we measure distance and time using the dimensionless variables X = x/λ and T = t/τ, the cable equation simplifies further to
Now, let’s see how Rall generalized this to a branching network. Instead of having one fiber, assume you have a variable number that depends on position along the network, n(x). Furthermore, assume the radius of each individual fiber varies, a(x). The cable equation can be derived as before, but because ri now varies with position (ri = 1/nπa2σ, where σ is the intracellular conductivity), we pick up an extra term
When I first looked at this equation, I thought “Aha! If ri is independent of x, the new term disappears and you get the plain old cable equation.” It’s not quite that simple; λ also depends on position, so even without the extra term this is not the cable equation. Remember, we want to measure distance in the dimensionless variable X = x/λ, but λ depends on position, so the relationship between derivatives of x and derivatives of X is complicated
If λri is constant along the axon, the ugly new term vanishes and you have the traditional cable equation. If you go back to the definition of ri and λ in terms of a and n, you find that this condition is equivalent to saying that na3/2 is constant along the network. If one fiber branches into two, the daughter fibers must each have a radius of 0.63 times the parent fiber radius. Dendritic trees that branch in this way act like a single fiber. This is Rall’s result: the Rall equivalent cylinder.
If you want to learn more about Rall’s work, read the book The Theoretical Foundation of Dendritic Function: Selected Papers of Wilfrid Rall with Commentaries, edited by Idan Segev, John Rinzel, and Gordon M. Shepherd. The foreword, by Terrence J. Sejnowski, says
The exploration of the electrical properties of dendrites by Wilfrid Rall provided many key insights into the computational resources of the neurons. Many of the papers in this collection are classics: dendrodendritic interactions in the olfactory bulb; nonlinear synaptic integration in motoneuron dendrites; active currents in pyramidal neuron apical dendrites. In each of these studies, insights arose from a conceptual leap, astute simplifying assumptions, and rigorous analysis. Looking back, one is impressed with the foresight shown by Rall in his choice of problems, with the elegance of his methods in attacking them, and with the impact that his conclusions have had for our current thinking. These papers deserve careful reading and rereading, for there are additional lessons in each of them that will reward the careful reader....It would be difficult to imagine the field of computational neuroscience today without the conceptual framework established over the last thirty years by Wil Rall, and for this we all owe him a great debt of gratitude.