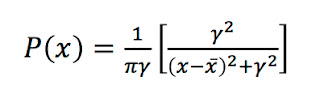In an appendix of Intermediate Physics for Medicine and Biology, Russ Hobbie and I analyze the Gaussian probability distribution
It has the classic bell shape, centered at mean x with a width determined by the standard deviation σ.
Other distributions have a similar shape. One example is the Cauchy distribution
where the distribution is centered at x and has a half-width at half-maximum γ. I initially thought the Cauchy distribution would be as well behaved as any other probability distribution, but it’s not. It has no mean and no standard deviation!
Rather than thinking abstractly about this issue, I prefer to calculate and watch how things fall apart. So, I wrote a simple computer program to generate N random samples using either the Gaussian or the Cauchy distribution. Below is a histogram for each case (N = 1000; Gaussian, x = 0, σ = 1; Cauchy, x = 0, γ = 1).
Those samples out on the wings of the Cauchy distribution are what screw things up. The probability falls off so slowly that there is a significant chance of having a random sample that is huge. The histograms shown above are plotted from −20 to 20, but one of the thousand Cauchy samples was about −2400. I’d need to plot the histogram over a range more than one hundred times wider to capture that bin in the histogram. Seven of the samples had a magnitude over one hundred. By contrast, the largest sample from the Gaussian was about 4.6.
What do these few giant samples do to the mean? The average of the thousand samples shown above obtained from the Cauchy distribution is −1.28, which is bigger than the half-width at half-max.
The average of the thousand samples obtained from the
Gaussian distribution is −0.021, which is much smaller than the standard deviation.
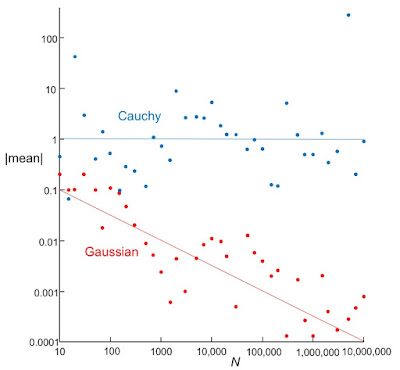
Even more interesting is how the mean varies with N. I tried a bunch of cases, summarized in the figure below.
There’s a lot of scatter, but the means for the Gaussian data appear to get smaller (closer to the expected value of zero) as N gets larger, The red line is not a fit, but merely drawn by eye. I included it to show how the means fall off with N. It has a slope of −½, implying that the means decay roughly as 1/√N. In contrast, the means for the Cauchy data are large (on the order of one) and don’t fall off with N. No matter how many samples you collect, your mean doesn’t approach the expected value of zero. Some oddball sample comes along and skews the average.
If you calculate the standard deviations for these cases, the problem is even worse. For data generated using the Cauchy distribution, the standard deviation grows with N. For N over a million, the standard deviation is usually over a thousand (remember, the half-width at half-max is one), and for my N = 5,000,000 case the standard deviation was over 600,000. Oddballs dominate the standard deviation.
I’m sorry if my seat-of-the-pants experimental approach to analyzing the Cauchy distribution seems simplistic, but for me it provides insight. The Cauchy distribution is weird, and I’m glad Russ and I didn’t include an appendix about it in Intermediate Physics for Medicine and Biology.
Friday, September 27, 2019
Friday, September 20, 2019
Happy Birthday Professor Fung
Yuan-Cheng Fung celebrated his 100th birthday last Sunday.
When Russ Hobbie and I needed to cite a general biomechanics textbook in Intermediate Physics for Medicine and Biology, we chose Biomechanics: Mechanical Properties of Living Tissues by “Bert” Fung.
Another of Fung’s books that I like is A First Course in Continuum Mechanics. He states his goal in its first sentence. It’s a similar goal to that of IPMB.
Fung joined the faculty at Caltech and remained there for nearly twenty years. In the 1950's, he became interested in biomechanics when his mother was suffering from glaucoma. In 1966, Fung moved to the University of California at San Diego, where he established their bioengineering program. He is known as the “Father of Modern Biomechanics.”
Happy birthday Professor Fung.
 |
| Biomechanics: Mechanical Properties of Living Tissues, by Y. C. Fung. |
Whenever a force acts on an object, it undergoes a change of shape or deformation. Often these deformations can be ignored… In other cases, such as the contraction of a muscle, the expansion of the lungs, or the propagation of a sound wave, the deformation is central to the problem and must be considered. This book will not develop the properties of deformable bodies extensively; nevertheless, deformable body mechanics is important in many areas of biology (Fung 1993).According to Google Scholar, Biomechanics has over 10,000 citations, implying it’s a very influential book. In his introduction, Fung writes
Biomechanics seeks to understand the mechanics of living systems. It is an ancient subject and covers a very wide territory. In this book we concentrate on physiology and medical applications, which constitute the majority of recent work in the field. The motivation for research in this area comes from the realization that physiology can no more be understood without biomechanics than an airplane can without aerodynamics. For an airplane, mechanics enables us to design its structure and predict its performance. For an organ, biomechanics helps us to understand its normal function, predict changes due to alterations, and propose methods of artificial intervention. Thus diagnosis, surgery, and prosthesis are closely associated with biomechanics.
 |
| A First Course in Continuum Mechanics, by Y. C. Fung. |
Our objective is to learn how to formulate problems in mechanics, and how to reduce vague questions and ideas to precise mathematical statements, as well as to cultivate a habit of questioning, analyzing, designing, and inventing in engineering and science.A special issue of the Journal of Biomechanical Engineering is dedicated to Fung’s birthday celebration. The editors write
Dr. Fung has been a singular pioneer in the field of Biomechanics, establishing multiple biomechanical theories and paradigms in various organ systems, including the heart, blood vessels, blood cells, and lung... He has mentored and trained many researchers in the biomechanics and bioengineering fields. His books … have become the classic biomechanics textbooks for students and researchers around the world. Dr. Fung is a member of all three U.S. National Academies—National Academy of Sciences, National Academy of Engineering, and National Academy of Medicine. He is also a member of the Chinese Academy of Sciences and a member of Academia Sinica. He has received many awards including the Timoshenko medal, the Russ Prize, and the National Medal of Science.Fung earned his bachelor’s and master's degrees in aeronautics from the Central University of China in 1941 and 1943. College must have been difficult in China during the Second World War. I bet he has stories to tell. After the war he won a scholarship to come to the United States and study at Caltech, where he earned his PhD in 1948.
Fung joined the faculty at Caltech and remained there for nearly twenty years. In the 1950's, he became interested in biomechanics when his mother was suffering from glaucoma. In 1966, Fung moved to the University of California at San Diego, where he established their bioengineering program. He is known as the “Father of Modern Biomechanics.”
Happy birthday Professor Fung.
Yuan-Cheng Fung: 2000 National Medal of Science
2007 Russ Prize video
Friday, September 13, 2019
Intermediate Physics for Medicine and Biology has a New Website
A New Website
This summer I received an email from University Technology Services saying that faculty websites, like the one I maintain about Intermediate Physics for Medicine and Biology, would no longer be supported at Oakland University. In other words, IPMB needed a new online home. So today I announce our new website: https://sites.google.com/view/hobbieroth. If you try to access the old website listed in IPMB, www.oakland.edu/~roth/hobbie, it’ll link you to the new site, but I don’t know how long that will last.What can you find at our new website? Lots of stuff, including
- Errata. The errata is a list of errors in IPMB.
- Blog. Information about this book blog, including the mapping of blog posts to sections in IPMB, which is useful if you want additional information about a particular topic.
- Links. Links to sites such as the IPMB Facebook group and the publisher webpage.
- Trivial Pursuit IPMB. Game cards for the board game that’s all the rage: Trivial Pursuit IPMB.
- MacDose. Links to MacDose, the computer program Russ Hobbie wrote to teach the interaction of radiation with matter.
Class Videos
This semester I’m teaching PHY 3250, Biological Physics. I am recording each class, and I’ll upload the videos to YouTube. Anyone can watch the lectures for free, as if it were an online class. I still use the blackboard, and sometimes it’s difficult to read in the video. I hope you can follow most of the lectures.
PHY 3250 class on September 6, 2019, covering biomechanics.
Useful for Instructors
If you scroll down to the box on the right of hobbieroth.blogspot.com you will find a list of labels. Click the one called “Useful for Instructors” and you can find several posts that are….er….useful for instructors. If you’re teaching from IPMB, you might find these posts particularly helpful.Google Scholar
Below is a screenshot of IPMB’s Google Scholar citation statistics. We’ve averaged 26 citations a year over the last ten years, or one every two weeks. We thank all of you who’ve referenced IPMB. We’re delighted you found it important enough to cite.Friday, September 6, 2019
The Linear No-Threshold Model of Radiation Risk
Certain topics discussed in Intermediate Physics for Medicine and Biology always fascinate me. One is the linear no-threshold model. In Section 16.12, Russ Hobbie and I write
The linear no-threshold assumption is debated in a point/counterpoint article in the August issue of Medical Physics (“The Eventual Rejection of the Linear No-Threshold Theory Will Lead to a Drastic Reduction in the Demand for Diagnostic Medical Physics Services,” Volume 46, Pages 3325-3328). I have discussed before how useful point/counterpoint articles are for teaching medical physics. They provide a glimpse into the controversies that medical physicists grapple with every day. The title of each point/counterpoint article is phrased as a proposition. In this case, Aaron Jones argues for the proposition and Michael O’Connor argues against it. The moderator Habib Zaidi frames the issue in his overview
The linear no-threshold model has little impact for individuals, but is critical for estimating public health risks—such as using backscatter x-ray detectors in airports—when millions of people are exposed to minuscule doses. I’m no expert on this topic so I can’t comment with much authority, but I’ve always been skeptical of the linear no-threshold model.
Much of this point/counterpoint article deals with the impact of the linear no-threshold model on the medical physics job market. I agree with O’Connor that “[The title of the point/counterpoint article] is an interesting proposition as it implies that medical physicists care only about their field and not about whether or not a scientific concept (the LNT) is valid or not,” except “interesting” is not the word I would have chosen. I am skeptical that resolution of the LNT controversy will have a significant consequences for medical physics employment. After we discuss a point/counterpoint article in my PHY 3260 (Medical Physics) class, I insist that students vote either "for" or "against" the proposition. In this case, I agree with O'Connor and vote against it.
I will leave you with O’Connor’s concluding speculation about how rejecting the linear no-threshold model will affect both the population at large and on the future medical physics job market.
In dealing with radiation to the population at large, or to populations of radiation workers, the policy of the various regulatory agencies has been to adopt the linear no-threshold (LNT) model to extrapolate from what is known about the excess risk of cancer at moderately high doses and high dose rates, to low doses, including those below natural background.Possible responses to radiation are summarized in Figure 16.51 of IPMB. Scientists continue to debate the LNT model because reliable data (shown by the two data points with their error bars in the upper right) do not extend down to low doses.
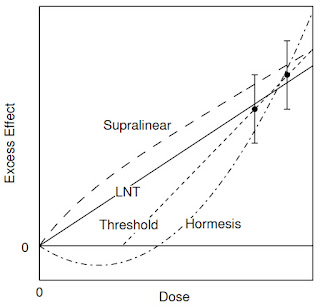 |
| Figure 16.51 from IPMB, showing possible responses to various doses. The two lowest-dose measurements are shown with their error bars. |
Controversies about the linear no‐threshold (LNT) hypothesis have been around since the early development of basic concepts in radiation protection and publication of guidelines by professional societies. Historically, this model was conceived over 70 yr ago and is still widely adopted by most of the scientific community and national and international advisory bodies (e.g., International Commission on Radiological Protection, National Council on Radiation Protection and Measurements) for assessing risk from exposure to low‐dose ionizing radiation. The LNT model is currently employed to provide cancer risk estimates subsequent to low level exposures to ionizing radiation despite being criticized as causing unwarranted public fear of all low-dose radiation exposures and costly implementation of unwarranted safety measures. Indeed, linearly extrapolated risk estimates remain hypothetical and have never been rigorously quantified by evidence-based studies. As such, is the LNT model legitimate and its use by regulatory and advisory bodies justified? What would be the impact on our profession if this hypothesis were to be rejected by the scientific community? Would this result in drastic reduction in the demand for diagnostic medical physics services? These questions are addressed in this month’s Point/Counterpoint debate.Both protagonists give little support to the linear no-threshold hypothesis; they write as if its rejection is inevitable. What is the threshold dose below which risk is negligible? This question is not resolved definitively, but 100 mSv is the number both authors mention.
The linear no-threshold model has little impact for individuals, but is critical for estimating public health risks—such as using backscatter x-ray detectors in airports—when millions of people are exposed to minuscule doses. I’m no expert on this topic so I can’t comment with much authority, but I’ve always been skeptical of the linear no-threshold model.
Much of this point/counterpoint article deals with the impact of the linear no-threshold model on the medical physics job market. I agree with O’Connor that “[The title of the point/counterpoint article] is an interesting proposition as it implies that medical physicists care only about their field and not about whether or not a scientific concept (the LNT) is valid or not,” except “interesting” is not the word I would have chosen. I am skeptical that resolution of the LNT controversy will have a significant consequences for medical physics employment. After we discuss a point/counterpoint article in my PHY 3260 (Medical Physics) class, I insist that students vote either "for" or "against" the proposition. In this case, I agree with O'Connor and vote against it.
I will leave you with O’Connor’s concluding speculation about how rejecting the linear no-threshold model will affect both the population at large and on the future medical physics job market.
In our new enlightened world 30 yr from now, LNT theory has long been discarded, the public are now educated as to the benefits of low doses of ionizing radiation and there is no longer a race to push radiation doses lower and lower in x‐ray imaging. On the contrary, with acceptance of radiation hormesis, a new industry has arisen that offers the public an annual booster dose of radiation every year, particularly if they live in low levels of natural background radiation. How will this booster dose be administered? For those with the means, it might mean an annual trip to the Rocky Mountains. For others it could mean a trip to the nearest clinic for a treatment session with ionizing radiation. Who will oversee the equipment designed to deliver this radiation, to insure that the correct dose is delivered? The medical physicist!
Subscribe to:
Posts (Atom)