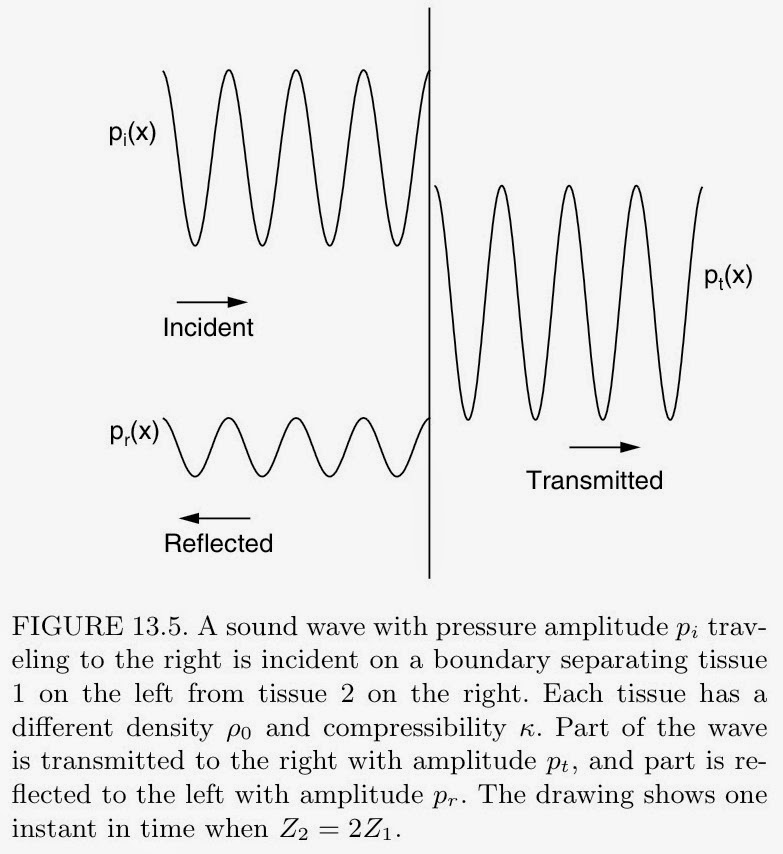
Figure 13.5

In Chapter 13 of the 4th edition of Intermediate Physics for Medicine and Biology, Russ Hobbie and I discuss imaging using ultrasound. One of the key concepts in this chapter is the reflection of an ultrasonic wave at the boundary between tissues having different acoustic impedances. The acoustic impedance is equal to the square root of ρ/κ, where ρ is the density and κ is the compressibility. An ultrasonic image is formed by recording echoes of an ultrasonic wave and using the timing of those echoes to determine the distance from tissue boundaries.

Figure 13.5 from Intermediate Physics for Medicine and Biology.

Figure 13.5 shows schematically how part of a pressure wave approaching a surface (the incident wave) passes through the surface (the transmitted wave) and part travels back toward the wave’s source (the reflected wave, or echo). When you look closely, however, there is something odd about this figure: the transmitted wave has a larger amplitude than the incident wave. How can this be? Doesn’t this violate some conservation law? If we consider particles rather than waves, we would expect that if 100 particles were incident on a surface, perhaps 75 of them would be transmitted and 25 reflected. Figure 13.5 seems to imply that 100 incident particles result in 133 transmitted and 33 reflected! How?

The figure is not wrong; the problem is with our intuition. Pressure is not a conserved quantity. There is no reason to expect the sum of the pressures of the transmitted and reflected waves to equal the pressure of the incident wave. The amplitudes are consistent with equations 13.26 and 13.27 in IPMB relating the three waves. Yet there is a conserved quantity, one we all know: energy.

The intensity of a wave is the energy per unit area per unit time. The intensity I, pressure p, and acoustic impedance Z are related by equation 13.29: I = p²/2Z. The transmitted wave in Fig. 13.5 has a pressure amplitude that is 1.33 times the amplitude of the incident wave, but it is moving through a tissue that has twice the acoustic impedance (the caption says that for this figure, Z₂ = 2 Z₁). For simplicity, take the acoustic impedance on the left (the incident side of the boundary, region 1) to be Z₁ = 0.5 and the amplitude of the incident wave to be p_i = 1 (let’s not worry about units for now, because our goal is to compare the relative intensities of the three waves). In this case, the intensity of the incident wave is equal to one. If the transmitted pressure is 1.33 and the acoustic impedance on the right (region 2) is Z₂ = 1 (twice Z₁), then the transmitted intensity is (1.33)²/2 = 0.89. The reflected wave has amplitude 0.33, and is propagating through the tissue on the left, so its intensity is (0.33)²/1 = 0.11. The sum of the intensities of the transmitted and reflected waves, 0.89 + 0.11, is equal to the intensity of the incident wave. Energy is conserved! The figure is correct after all.

Here is another way to think about intensity: it’s one half of the product of the pressure times the tissue speed. When I say “tissue speed” I don’t mean the propagation speed of the wave, but the speed of the tissue itself as it oscillates back and forth. The acoustic impedance relates the pressure and tissue speed. The large pressure of the transmitted wave is associated with a small tissue speed. The transmitted wave in Fig. 13.5 looks “big” only because we plot the pressure. Had we plotted tissue speed instead, we would not be wondering why the transmitted wave has such a large amplitude. We would, however, be scratching our head about a funny phase shift in the reflected wave, which the version of the figure showing the pressure hides.

So, Fig. 13.5 is correct. Does that mean it looks exactly the same in the 5th edition of IPMB (due out this summer)? No, we did change the figure; not to correct an error, but to emphasize another point. Figure 13.5, as presently drawn, shows the wavelength of the transmitted wave to be the same as the wavelength of the incident wave. The wavelength does not depend on the acoustic impedance, but it does depend on the wave speed (the propagation speed of the wave itself, usually given the symbol c, which is not the same as the speed of the oscillating tissue). The wave speed is equal to the square root of the reciprocal of the product of the density and compressibility. One can cook up examples where two tissues have the same wave speed but different acoustic impedances. For instance (again, not worrying about units and only comparing relative sizes), if the tissue on the left had twice the compressibility and half the density of the tissue on the right, then the left would have half the acoustic impedance and the same wave speed as the right, just as shown in Fig. 13.5. But tissues usually differ in compressibility by a greater factor than they differ in density. If we assume the two regions have the same density but the right has one-fourth the compressibility, then Z₂ = 2 Z₁ as before but also c₂ = 2 c₁, so the wavelength is longer on the right. In the 5th edition, the figure now shows the wavelength longer on the right.

What is the moral to this story? Readers (and authors) need to think carefully about illustrations such as Fig. 13.5. They tell a physical story that is often richer and more complicated than we may initially realize.

Physical Models of Living Systems

Physical Models of
Living Systems,
by Philip Nelson.

Philip Nelson has a new textbook that came out earlier this year: Physical Models of Living Systems. It’s an excellent book, well written and beautifully illustrated. The target audience is similar to that for the 4th edition of Intermediate Physics for Medicine and Biology: upper-level undergraduates who have studied physics and math at the introductory level. Like IPMB, it stresses the construction of physical and mathematical models of living systems.

At the start of the book, Nelson provides a section labeled “To the Student.” I hope students read this, as it provides much wisdom and advice. In fact, most of this advice applies as well to IPMB. I found his discussion of “skills” to be so valuable that I reproduce it here.

Science is not just a pile of facts for you to memorize. Certainly you need to know many facts, and this book will supply some as background to the case studies. But you also need skills. Skills cannot be gained just by reading through this (or any) book. Instead you’ll need to work through at least some of the exercises, both those at the ends of chapters and others sprinkled throughout the text.

Specifically, this book emphasizes

• Model construction skills: It's important to find an appropriate level of description and then write formulas that make sense at that level. (Is randomness likely to be an essential feature of this system? Does the proposed model check out at the level of dimensional analysis?) When reading others’ work, too, it’s important to be able to grasp what assumptions their model embodies, what approximations are being made, and so on.

• Interconnection skills: Physical models can bridge topics that are not normally discussed together, by uncovering a hidden similarity. Many big advances in science came about when someone found an analogy of this sort.

• Critical skills: Sometimes a beloved physical model turns out to be . . . wrong. Aristotle taught that the main function of the brain was to cool the blood. To evaluate more modern hypotheses, you generally need to understand how raw data can give us information, and then understanding.

• Computer skills: Especially when studying biological systems, it’s usually necessary to run many trials, each of which will give slightly different results. The experimental data very quickly outstrip our abilities to handle them by using the analytical tools taught in math classes. Not very long ago, a book like this one would have to content itself with telling you things that faraway people had done; you couldn’t do the actual analysis yourself, because it was too difficult to make computers do anything. Today you can do industrial-strength analysis on any personal computer.

• Communication skills: The biggest discovery is of little use until it makes it all the way into another person’s brain. For this to happen reliably, you need to sharpen some communication skills. So when writing up your answers to the problems in this book, imagine that you are preparing a report for peer review by a skeptical reader. Can you take another few minutes to make it easier to figure out what you did and why? Can you label graph axes better, add comments to your code for readability, or justify a step? Can you anticipate objections?

You'll need skills like these for reading primary research literature, for interpreting your own data when you do experiments, and even for evaluating the many statistical and pseudostatistical claims you read in the newspapers.

One more skill deserves separate mention. Some of the book’s problems may sound suspiciously vague, for example, “Comment on . . .” They are intentionally written to make you ask, “What is interesting and worthy of comment here?” There are multiple “right” answers, because there may be more than one interesting thing to say. In your own scientific research, nobody will tell you the questions. So it’s good to get the habit of asking yourself such things.

Nelson begins the book by discussing virus dynamics, and specifically analyzes the work of Alan Perelson, who constructs mathematical model of how the human immunodeficinecy virus interacts with our immune system. Here at Oakland University, Libin Rong (a former postdoc of Perelson’s) does similar research, and their work is an excellent case study in using mathematics to model a biological process.

A large fraction of the book examines the role of randomness in biology, leading to a detailed analysis of probability. Nelson provides an elegant discussion of the experiments of Max Delbruck and Salvador Luria.

S. Luria and M. Delbruck set out to explore inheritance in bacteria in 1943. Besides addressing a basic biological problem, this work developed a key mode of scientific thought. The authors laid out two competing hypotheses, and sought to generate testable quantitative predictions from them. But unusually for the time, the predictions were probabilistic in character. No conclusion can be drawn from any single bacterium—sometimes it gains resistance; usually it doesn’t. But the pattern of large numbers of bacteria has bearing on mechanism. We will see how randomness, often dismissed as an unwelcome inadequacy of an experiment, turned out to be the most interesting feature of the data.

Perhaps one way to appreciate the differences between Physical Models of Living Systems and IPMB is to compare how each handles diffusion. Russ Hobbie and I consider diffusion in Chapter 4 of IPMB; we describe diffusion as arising from a concentration gradient (Fick’s first law), and use the continuity equation to derive the diffusion equation (Fick’s second law). These relationships are macroscopic descriptions of diffusion. Then, at the end of the chapter—almost as an afterthought—we show that diffusion can be thought of as a random walk. Nelson, on the other hand, starts by analyzing the random nature of diffusion using probabilistic ideas, and then—almost as an afterthought—derives the diffusion equation (or at least a discrete approximation of it). I think this example reflects the different approaches of the two books: IPMB generally takes a macroscopic approach but sometimes reaches down with an example at the microscopic level, whereas Physical Models in Living Systems typically starts with a microscopic description and then sometimes works its way up to the macroscopic level.

Both books also have an extensive analysis of feedback. The canonical example in IPMB comes from physiology at the organism level: breathing rate controls and is controlled by blood carbon dioxide concentration. In Physical Models in Living Systems, a central example is how bacteria use feedback to regulate the synthesis of the amino acid tryptophan. Both case studies are excellent examples of negative feedback, but at different spatial scales. One example is not better than the other; they’re merely different illustrations of the same idea.

One strength of Physical Models of Living Systems is its emphasis on using computer simulations to describe a system’s behavior. IPMB has a few computer programs (for example, a program is provided to simulate the Hodgkin-Huxley model of a nerve axon), but Physical Models of Living Systems has a much heavier reliance on numerical simulation. Again, one approach isn’t better than the other, just different. One can learn a lot about biology using toy models and analytical analysis, but many more-complicated (often nonlinear) processes need the numerical approach. Anyone who uses, or plans to use, MATLAB for simulations may benefit from the Student’s Guide to Physical Models of Living Systems (available free to all at www.macmillanhighered.com/physicalmodels1e).

In conclusion, Nelson states that Physical Models of Living Systems is about how “physical science and life science illuminate each other,” and I can’t think of a better description of the goal of Intermediate Physics for Medicine and Biology. Students are lucky they have both to choose from. Finally, what is the very best thing about Physical Models of Living Systems? At the end of the “To the Student” section, Nelson lists several other books that complement his, and cites…you guessed it…Intermediate Physics for Medicine and Biology.

The Steradian

Angles are measured in radians, but solid angles are measured in steradians. Russ Hobbie and I discuss solid angles in Appendix A of the 4th edition of Intermediate Physics for Medicine and Biology.

A plane angle measures the diverging of two lines in two dimensions. Solid angles measure the diverging of a cone of lines in three dimensions. Figure A.3 shows a series of rays diverging from a point and forming a cone. The solid angle Ω is measured by constructing a sphere of radius r centered at the vertex and taking the ratio of the surface area S on the sphere enclosed by the cone to r²:

Ω = S/r².

…The unit of solid angle is the steradian (sr). A complete sphere subtends a solid angle of 4π steradians, since the surface area of a sphere is 4πr².

It is useful to have an intuitive idea of how big a steradian is. Viewed from the center of the earth, Asia subtends about one steradian, and Switzerland subtends about one millisteradian. From its center a sphere subtends 4π steradians, so one steradian is 1/4π = 0.08, or 8% of the sphere area. Suppose we use spherical coordinates to determine the area, centered at the north pole (θ = 0), that subtends one steradian. It is the area subtended by the “cap” of the sphere having an angle θ = cos^-1(1-1/2π) = cos^-1(0.84) = 32.8 degrees, or 0.57 radians.

One square degree is (π/180)² = 0.000305 sr = 305 μsr. In other words, there are 3283 square degrees per steradian. Put in yet another way, a steradian is one square radian. The moon has a radius of 1737 km, and the distance between the earth and the moon is 384,400 km. The solid angle subtended by the moon in the night sky is therefore π 1737²/384400² = 0.000064 sr, or 64 μsr. Interestingly, the sun, with a radius of 696,000 km and an earth-sun distance of 149,600,000 km, subtends almost the same solid angle, which makes solar eclipses so interesting. Viewed from earth, Mars at its closest approach subtends about 12 nanosteradians.

At the Battle of Bunker Hill, the order went out to “don't fire until you see the whites of their eyes.” This may be a figure of speech, but let’s take it literally. You can see the whites of a person’s eyes at a distance of about 10 meters (I would definitely be shooting before the enemy got that close). The area of the “whites of the eye” is difficult to estimate accurately, but let’s approximate it as one square centimeter. What solid angle is subtended by the whites of the eye at a distance of ten meters? It would be about (0.01 m)²/(10 m)², or one microsteradian. This is not bad for an estimate of our visual acuity. We may sometimes do a little better than this, but probably not during battle.

On Writing Well

Oakland University, where I work, has an ADVANCE grant from the National Science Foundation, with the goal of increasing the representation and advancement of women in academic science and engineering careers. I am part of the leadership team for the Women in Science and Engineering at Oakland University (WISE@OU) Program, and one of my roles is to help mentor young faculty. Last Tuesday I led a WISE@OU workshop on “Best Practices in Scientific Writing.” The event was videotaped, and you can watch it here. I’m the bald guy who is standing and wearing the red shirt.

On Writing Well,
by William Zinsser.

A list of writing resources was provided to all workshop participants (see below). It begins “For the most benefit in the least time with no cost, work through the Duke online Scientific Writing Resource, then read Part 1 (about 50 pages) of Zinsser’s book On Writing Well (available free online), and finally go through the online material for the Stanford Writing in the Sciences class.” If you don’t have enough time for even these three steps, then just read Zinsser, which is a delight.
Russ Hobbie and I try to write well in the 4th edition of Intermediate Physics for Medicine and Biology. You can decide if we succeed. Many readers of this blog are from outside the United States (I can tell from the “likes” on the book’s Facebook page). As I noted in the workshop, it is not fair that scientists from other countries must write science in a language other than their native tongue. Yet, most science is published in English, and scientists need to be able to write it well. So, my advice is to do whatever it takes to become a decent writer.

When I was in graduate school, my dissertation advisor John Wikswo gave me a copy of The Complete Plain Words, a wonderful book about writing originally published by Sir Ernest Gowers. Read it for free online. The version Wikswo loaned me was a later edition coauthored by Bruce Fraser. (You always should be concerned when a perfectly good book picks up a coauthor in later editions). This spring, Gowers’ great-granddaughter Rebecca Gowers is publishing a new edition of Plain Words. I can’t wait. Another oldie but goodie is Strunk and White’s The Elements of Style. The original, by William Strunk, is available online. (The second author of “Strunk and White” is E. B. White who wrote Charlotte’s Web; I vividly remember Mrs. Sheets reading Charlotte’s Web aloud to my third grade class at Northside Elementary School.) If you have time for only three words about writing, let them be Strunk’s admonition “omit needless words.”

I’ve come up with my own Three Laws of Writing Science, patterned after Isaac Asimov’s Three Laws of Robotics (regular readers of this blog know that Asimov influenced me greatly when I was in high school).

• First Law: What you write must be scientifically correct. 

• Second Law: Write clearly, except when clarity would put you in conflict with the First Law.

• Third Law: Write concisely, except when conciseness would put you in conflict with the First or Second Laws.

Writing is easier when you enjoy doing it, and I always have. I once became secretary of the Parent-Teacher Association at my daughters’ elementary school because that job allowed me to write the minutes of the PTA meetings. If you don’t enjoy writing, take heart. You don’t need to be a great writer to succeed in science. Slipping into NSF-speak, if you can improve from “poor” or “fair” to “good” you will get almost the full benefit. Go from “good” to “very good” or “excellent” only if you like to write.

Best Practices in Scientific Writing

Below is a list of resources about scientific writing. For the most benefit in the least time with no cost, work through the Duke online Scientific Writing Resource, then read Part 1 (about 50 pages) of Zinsser’s book On Writing Well (available free online), and finally go through the online material for the Stanford Writing in the Sciences class.

Books about writing:

• Gowers R, Gowers E. 2014. Plain Words
• Gray-Grant D. 2008. 8 ½ Steps to Writing Better, Faster
• Pinker, S. 2014. The Sense of Style
• Silvia PJ. 2007. How to Write a Lot 
• Strunk W, White EB. 1979. The Elements of Style
• Zinsser W. 1976. On Writing Well (free online: archive.org/details/OnWritingWell)

American Scientist article “The Science of Scientific Writing”

Video of Steven Pinker discussing good writing

A free online course from Stanford about Writing in the Sciences

Kamat, Buriak, Schatz, Weiss. 2014. “Mastering the art of scientific publicaition: Twenty papers with 20/20 vision on publishing,” J. Phys. Chem. Lett., 5:3519–3521.

Kotz, Cals, Tugwell, Knottnerus. 2013. “Introducing a new series on effective writing and publishing of scientific papers,” J. Clinical Epidemiology, 66:359–360.

How to Get Published. A discussion with Mike Sevilla and myself, moderated by George Corser, about writing and publishing scientific papers, hosted the OU graduate student group GradConnection.

A free online webinar debating the use of the active or passive voice

Duke University’s online Scientific Writing Resource, open to all.

Nonnative English speakers (and the rest of us too) should see the website Scientific English as a Foreign Language.