If the [magnetic] signal is strong enough, it can be detected with conventional coils and signal-averaging techniques that are described in Chap. 11. Barach et al. (1985) used a small detector through which a single axon was threaded. The detector consisted of a toroidal magnetic core wound with many turns of fine wire... Current passing through the hole in the toroid generated a magnetic field that was concentrated in the ferromagnetic material of the toroid. When the field changed, a measurable voltage was induced in the surrounding coil. This neuromagnetic current probe has been used to study many nerve and muscle fibers (Wijesinghe 2010).I have discussed the neuromagnetic current probe before in this blog. One of the best places to learn more about it is a paper by Frans Gielen, John Wikswo, and me in the IEEE Transactions on Biomedical Engineering (Volume 33, Pages 910–921, 1986). The paper begins
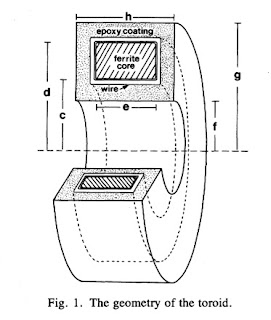
In one-dimensional tissue preparations, bioelectric action currents can be measured by threading the tissue through a wire-wound, ferrite-core toroid that detects the associated biomagnetic field. This technique has several experimental advantages over standard methods used to measure bioelectric potentials. The magnetic measurement does not damage the cell membrane, unlike microelectrode recordings of the internal action potential. Recordings can be made without any electrical contact with the tissue, which eliminates problems associated with the electrochemistry at the electrode-tissue interface. While measurements of the external electric potential depend strongly on the distance between the tissue and the electrode, measurements of the action current are quite insensitive to the position of the tissue in the toroid. Measurements of the action current are also less sensitive to the electrical conductivity of the tissue around the current source than are recordings of the external potential.Figure 1 of this paper shows the toroid geometry
where μ is the magnetic permeability. The question is, what value should I use for r? Should I use the inner radius, the outer radius, the width, or some combination of these? The answer can be found by solving this new homework problem.
Section 8.2
Problem 11 1/2. Suppose a toroid having inner radius c, outer radius d, and width e is used to detect current i in a wire threading the toroid’s center. The voltage induced in the toroid is proportional to the magnetic flux through its cross section.
(a) Integrate the magnetic field produced by the current in the wire across the cross section of the ferrite core to obtain the magnetic flux.
(b) Calculate the average magnetic field in the toroid, which is equal to the flux divided by the toroid cross-sectional area.
(c) Define the “effective radius” of the toroid, reff, as the radius needed in Eq. 8.7 to relate the current in the wire to the average magnetic field. Derive an expression for reff in terms of the parameters of the toroid.
(d) If c = 1 mm, d = 2 mm, e = 1 mm, and μ=104μo, calculate reff.The solution to this homework problem, the effective radius, appears on page 915 of our paper.
Finally, and just for fun, below I reproduce the short bios published with the paper, which appeared 30 years ago.