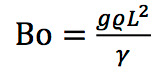Write Mind

Write Mind, by Eric Maisel.

Every Saturday morning my wife and I visit the Rochester Hills Public Library. I like to browse the stacks, and sometimes I find a gem. Recently, I checked out Write Mind: 299 Things Writers Should Never Say to Themselves (and What They Should Say Instead) by Eric Maisel.

Write Mind contains some cognitive therapy jargon that I don’t care for, but its second sentence quotes Epictetus so it can’t be all bad. Seriously, at its core this delightful book is about attitude. Not all problems can be solved by a positive attitude but some can, whether you are an aspiring writer or a struggling physics student.

Write Mind is aimed at writers. Two hundred and ninety nine times it first states an incorrect, negative attitude (WRONG MIND) and then a better, positive attitude (RIGHT MIND).

To help students of Intermediate Physics for Medicine and Biology I have paraphrased Write Mind, providing 29 pairs of statements about physics applied to medicine and biology. Forgive me if sometimes they are corny; I hope you find them useful.

1. 

WRONG MIND: Mathematics and medicine are so different; I can’t learn both so I’ll settle for one or the other.

RIGHT MIND: I can master both mathematics and medicine.

2. 

WRONG MIND: Physiology requires so much memorization! I will give up and stick to physics.

RIGHT MIND: I can learn both physics and physiology.

3. 

WRONG MIND: I hate toy models because they oversimplify biology.

RIGHT MIND: I will gain insight from a toy model, and then analyze its strengths and weaknesses.

4. 

WRONG MIND: I have difficulty understanding what some homework problems are asking; I skip those.

RIGHT MIND: Research problems are often ill-defined. I will try my best to understand the question and then answer it.

5. 

WRONG MIND: Robert Plonsey, Art Winfree, and John Wikswo have contributed so much; I can never accomplish that much in my career.

RIGHT MIND: I intend to work hard, and take Plonsey, Winfree, and Wikswo as role models.

6. 

WRONG MIND: I’m good at math and I love medicine, but I have trouble connecting the two.

RIGHT MIND: Homework problems let me practice connecting math to medicine. Many students struggle with this difficulty. I am not alone.

7. 

WRONG MIND: IPMB and its blog recommend so many books; I don’t have time to read them all, so I won’t read any.

RIGHT MIND: I will find time to read one of the books recommended in IPMB or its blog. Once I have finished it, I will try to find time for another.

8. 

WRONG MIND: I like IPMB but I don’t have time to do the homework problems.

RIGHT MIND: Today I’ll make time to solve four homework problems. Tomorrow, four more.

9. 

WRONG MIND: You have to be a genius to apply physics and mathematics to biology and medicine; I have no chance.

RIGHT MIND: I can learn to apply physics and math to biology and medicine.

10. 

WRONG MIND: I am a biologist, and biologists can’t do math.

RIGHT MIND: I intend to learn math.

11. 

WRONG MIND: I love math, but my premed advisor says I don’t need math to become a medical doctor.

RIGHT MIND: I choose to learn math and to become a medical doctor.

12. 

WRONG MIND: Some students learn the topics in IPMB easily, but for me they are difficult. I am not meant to understand this subject.

RIGHT MIND: I can understand the topics in IPMB if I work hard.

13. 

WRONG MIND: Applying physics and mathematics to medicine and biology is difficult; I need so many skills. It isn’t worth it. I give up.

RIGHT MIND: I am learning how to apply physics and math to medicine and biology. I’m seeing how it all fits together. It’s so cool!

14. 

WRONG MIND: I got my homework back and it was covered with red ink. My instructor is an ass.

RIGHT MIND: I got my homework back and my instructor made many corrections. Such valuable feedback!

15. 

WRONG MIND: I spent 30 minutes solving a differential equation. After all that effort, I doubt my solution is correct.

RIGHT MIND: I spent 30 minutes solving a differential equation. Now I will spend 3 minutes plugging my solution back into the differential equation to check that it really works.

16. 

WRONG MIND: I solved the differential equation. The solution is complicated and I don’t understand what it means physically.

RIGHT MIND: I solved the differential equation. Now I will examine limiting cases to understand what it means physically.

17. 

WRONG MIND: My homework is due Friday. I don’t have to start working on it until Thursday night.

RIGHT MIND: My homework is due Friday. I will start working on it on Monday, leaving time to ask questions if I get stuck.

18. 

WRONG MIND: I need to read books by Steven Vogel, Mark Denny, and Knut Schmidt-Nielsen before I am ready to begin my homework.

RIGHT MIND: I would love to read books by Vogel, Denny, and Schmidt-Nielsen, but first I really need to start my homework.

19.

WRONG MIND: I know how to compute an answer to the homework, but it doesn’t mean anything.

RIGHT MIND: The purpose of computation is insight. I will think about my answer until I understand it physically.

20.

WRONG MIND: I have taken a calculus course, but I didn't really master the subject. IPMB uses calculus a lot; I shouldn’t take a course based on it.

RIGHT MIND: I will take a course based on IPMB, and use the experience to improve my math skills.

21.

WRONG MIND: Real-world problems are so complicated. The toy models presented in IPMB won’t prepare me for complex real-world problems.

RIGHT MIND: Solving toy models will help me build the skills and intuition I need to successfully attack more complicated real-world problems.

22.

WRONG MIND: To solve a homework problem, I search for an equation to put numbers into: “plug-and-chug.”

RIGHT MIND: I will think before I calculate. After I calculate, I will think if my answer makes sense. I will always think.

23.

WRONG MIND: Some homework problems ask me to “estimate” something, but they don’t give me all the data I need. What a bunch of BS.

RIGHT MIND: Part of learning to estimate is to make reasonable assumptions about data I do not have. I will develop this skill.

24.

WRONG MIND: I derived a complicated equation. I have no idea if it is correct.

RIGHT MIND: I will check my equation by verifying that it has the correct units. This doesn’t prove it’s right, but it could prove it’s wrong. I will practice this skill.

25.

WRONG MIND: Why does IPMB derive so many equations? I don’t need the derivation; I just want to use the equation to calculate numbers.

RIGHT MIND: A derivation is like a story. The derivation explains what is happening physically, and reminds me what assumptions were made.

26.

WRONG MIND: IPMB is always using math to model biological phenomena. This bugs me, and I dislike using “model” as a verb.

RIGHT MIND: I need to be able to build simple mathematical models of biological phenomena. I must learn to model.

27.

WRONG MIND: The computed tomography algorithms that create an image from projections are beautiful. I could never discover something that profound.

RIGHT MIND: With much hard work, I intend to discover something new. I will use those beautiful computed tomography algorithms to motivate me.

28.

WRONG MIND: I received a C- on my first exam, and a D+ on the second. I quit.

RIGHT MIND: I have learned so much from my mistakes on the first two exams. Had I gotten A’s on those exams, I wouldn’t be pushing myself hard enough.

29.

WRONG MIND: The homework is difficult for me, and my exam average is a C+. I will never achieve my goal of making new and valuable contributions to biomedical engineering.

RIGHT MIND: The skills needed in research are not identical to those needed in the classroom. I have as much to contribute on the job as the A student.

WRONG MIND: I would love to write. RIGHT MIND: I intend to write.

Mathematics is Biology’s Next Microscope, Only Better; Biology is Mathematics’ Next Physics, Only Better

Intermediate Physics for Medicine and Biology is full of equations. Equations are on almost every page, and often lots of them. Russ Hobbie and I use calculus without apology, and we discuss differential equations, Fourier analysis, and vector calculus. To understand biology, must we use all this mathematics?

“Mathematics is Biology’s Next Microscope, Only Better;
Biology is Mathematics’ Next Physics, Only Better”

The answer given by Joel Cohen of Rockefeller University is Yes! In his 2004 article “Mathematics is Biology’s Next Microscope, Only Better; Biology is Mathematics’ Next Physics, Only Better” (PLoS Biol 2:e439), Cohen argues that math skills are crucial for modern biologists. He writes

Although mathematics has long been intertwined with the biological sciences, an explosive synergy between biology and mathematics seems poised to enrich and extend both fields greatly in the coming decades.

The first half of his argument I believe enthusiastically: math has much to offer biology.

Mathematics broadly interpreted is a more general microscope. It can reveal otherwise invisible worlds in all kinds of data... For example, computed tomography can reveal a cross-section of a human head from the density of X-ray beams without ever opening the head, by using the Radon transform [see Chapter 12 of IPMB] ... Charles Darwin was right when he wrote that people with an understanding “of the great leading principles of mathematics… seem to have an extra sense”... Today’s biologists increasingly recognize that appropriate mathematics can help interpret any kind of data. In this sense, mathematics is biology’s next microscope, only better.

In IPMB, Russ and I illustrate how mathematical models can describe biological and medical systems. We don’t use sophisticated or complicated math, but instead focus on toy models that train students to analyze biological problems quantitatively. On the first day of my Biological Physics class, I tell the students that the course is a workshop on applying simple mathematical models to biological phenomena. Mathematics really is biology’s next microscope.

The second half of Cohen’s argument is not as obvious. Will biology lead to new advances in mathematics?

In the coming century, biology will stimulate the creation of entirely new realms of mathematics. In this sense, biology is mathematics’ next physics, only better. Biology will stimulate fundamentally new mathematics because living nature is qualitatively more heterogeneous than non-living nature.

Well, maybe, but I am skeptical. Cohen claims that biology generates large amounts of data, and biological systems are diverse and heterogeneous, which will lead to new math concepts that deal with what we now call Big Data. I hope this is true, but I expect much of the math already exists. Perhaps my skepticism arises because I love simple models, and the new math will certainly be elaborate and abstruse. We will see.

In his article, Cohen does more than make general claims; he gives specific examples. For instance, he tells a lovely story about how simple mathematical reasoning led William Harvey to predict the existence of capillaries

[Harvey’s] theoretical prediction, based on his meticulous anatomical observations and his mathematical calculations, was spectacularly confirmed more than half a century later when Marcello Malpighi (1628–1694) saw the capillaries under a microscope. Harvey’s discovery illustrates the enormous power of simple, off-the-shelf mathematics combined with careful observation and clear reasoning. It set a high standard for all later uses of mathematics in biology.

I encourage you all to read Cohen’s article. It makes a persuasive case that books such as Intermediate Physics for Medicine and Biology are necessary and even essential. Enjoy!

Marie Curie and her X-ray Vehicles’ Contribution to World War I Battlefield Medicine

Sunday is Veterans Day. This year the holiday is particularly significant because it marks the 100th anniversary of the armistice ending World War I.

Marie Curie in a Mobile Military Hospital X-Ray Unit.

Readers of Intermediate Physics for Medicine and Biology might wonder how the Great War influenced the application of physics to medicine. Timothy Jorgensen published a fascinating article on the website The Conversation discussing Nobel Prize-winner Marie Curie’s use of medical x-rays on the battlefield. Below are some annotated excerpts.

[In addition to her discovery of radium and polonium, Curie (1867-1934)] was also a major hero of World War I. In fact, a visitor to her Paris laboratory 100 years ago would not have found either her or her radium on the premises. Her radium was in hiding and she was at war.

The Guns of August,by Barbara Tuchman.

For Curie, the war started in early 1914, as German troops headed toward her hometown of Paris [“early” 1914? Germany declared war against France on August 3; see Guns of August by Barbara Tuchman]…[Curie] gathered her entire stock of radium, put it in a lead-lined container, transported it by train to Bordeaux…and left it in a safety deposit box at a local bank…

With the subject of her life’s work hidden far away…she decided to redirect her scientific skills toward the war effort; not to make weapons, but to save lives.

X-rays...had been discovered in 1895 by Curie’s fellow Nobel laureate, Wilhelm Roentgen.… Almost immediately after their discovery, physicians began using X-rays to image patients’ bones and find foreign objects – like bullets. But at the start of the war, X-ray machines were still found only in city hospitals, far from the battlefields where wounded troops were being treated. Curie’s solution was to invent the first “radiological car” – a vehicle containing an X-ray machine and photographic darkroom equipment – which could be driven right up to the battlefield where army surgeons could use X-rays to guide their surgeries....

[As the war progressed,] more radiological cars were needed. So Curie exploited her scientific clout to ask wealthy Parisian women to donate vehicles. Soon she had 20, which she outfitted with X-ray equipment. But the cars were useless without trained X-ray operators, so Curie started to train women volunteers. She recruited 20 women for the first training course, which she taught along with her daughter Irene [1897-1956, making her a teenager during much of the war], a future Nobel Prize winner herself….

Not content just to send out her trainees to the battlefront, Curie herself had her own “little Curie” [Petites Curies] – as the radiological cars were nicknamed – that she took to the front. This required her to learn to drive, change flat tires and even master some rudimentary auto mechanics, like cleaning carburetors. And she also had to deal with car accidents. When her driver careened into a ditch and overturned the vehicle, they righted the car, fixed the damaged equipment as best they could and got back to work [don’t you just love her?]....

Curie survived the war but was concerned that her intense X-ray work would ultimately cause her demise. Years later, she did contract aplastic anemia, a blood disorder sometimes produced by high radiation exposure. Many assumed that her illness was the result of her decades of radium work – it’s well-established that internalized radium is lethal [see The Radium Girls by Kate Moore]. But Curie was dismissive of that idea. She had always protected herself from ingesting any radium. Rather, she attributed her illness to the high X-ray exposures she had received during the war. (We will likely never know whether the wartime X-rays contributed to her death in 1934, but a sampling of her remains in 1995 showed her body was indeed free of radium.)

To learn more about Marie Curie, I recommend Jorgensen’s fine book Strange Glow: The Story of Radiation, or the article about Marie and her husband Pierre Curie and the discovery of polonium and radium, published by the Nobel Prize website. If you are a child at heart and enjoy Animated Hero Classic videos, watch this tearjerker.

To learn more about x-ray imaging, see Intermediate Physics for Medicine and Biology:

Chapter 16 describes the use of x rays for medical diagnosis and treatment. It moves from production to detection, to the diagnostic radiograph. We discuss image quality and noise, followed by angiography, mammography, fluoroscopy, and computed tomography. After briefly reviewing radiobiology, we discuss therapy and dose measurement. The chapter closes with a section on the risks from radiation.

To learn more about the First World War, visit the National World War I Museum and Memorial in Kansas City (know locally as Liberty Memorial).

National World War I Museum and Memorial in Kansas City.

Happy Veterans Day all who have defended our country in the military (including my dad and my brother-in-law). Thank you for your service.

Roderick MacKinnon's Nobel Lecture

In Chapter 9 of Intermediate Physics for Medicine and Biology, Russ Hobbie and I write

Roderick MacKinnon and his colleagues determined the three-dimensional structure of a potassium channel using X-ray diffraction (Doyle et al. 1998; Jiang et al. 2003). MacKinnon received the 2003 Nobel Prize in Chemistry for his work on the potassium channel.

When I teach my graduate class on bioelectricity, we read the Doyle et al. article (“The Structure of the Potassium Channel: Molecular Basis of K⁺ Conduction and Selectivity,” Science, Volume 280, Pages 69–77, 1998). In my class, usually either my students and I discuss a paper or I explain some aspect of it. However, I’ve not found a better way to describe potassium channels than to watch MacKinnon’s brilliant Nobel lecture. I suggest you watch it too, using the embedded Youtube link below. It's 45 minutes long, but well worth the time.

If you have no time to spare, listen to the much shorter (less than two minute) interview where MacKinnon explains how being a scientist is like being an explorer.

Enjoy!

 

Roderick MacKinnon’s Nobel lecture.

 

“Being a scientist is like being an explorer.”

 

Earl Bakken (1924-2018)

Earl Bakken. From the Bakken Museum, via wikipedia.

Earl Bakken, cofounder of the medical device company Medtronic, died Sunday at the age of 94. In 1957 he developed the first external, battery-operated artificial pacemaker. Russ Hobbie and I don’t mention Bakken by name in Intermediate Physics for Medicine and Biology, but we do discuss pacemakers.

Cardiac pacemakers are a useful treatment for certain heart diseases. The most frequent are an abnormally slow pulse rate (bradycardia) associated with symptoms such as dizziness, fainting (syncope), or heart failure. These may arise from a problem with the SA node (sick sinus syndrome) or with the conduction system (heart block). One of the first uses of pacemakers was to treat complete or third degree heart block. The SA node and the atria fire at a normal rate but the wave front cannot pass through the conduction system. The AV node or some other part of the conduction system then begins firing and driving the ventricles at its own, pathologically slower rate…. A pacemaker stimulating the ventricles can be used to restore a normal ventricular rate.

In the 1950s, famed cardiac surgeon Dr. Walt Lillehei was at the University of Minnesota, where he met Bakken. Kirk Jeffrey tells the story of their collaboration in Machines In Our Hearts.

Machines In Our Hearts, by Kirk Jeffrey

The myocardial pacing wire was the first electrical device ever to be implanted in the human body and left there for a period of time. Surgeons at Minnesota were now able to pace children for days or weeks after heart surgery. By October 1957, they had used the technique with 18 patients. But Lillehei now grew uneasy about the Grass stimulator because it was bulky and plugged into the electrical system. The surgeon wanted to get his heart patients out of bed and moving around, but the stimulator had to accompany them on a wheeled cart. The electrical cord was a further nuisance. ‘‘Many of these [patients] were kids. They wanted to wander around and get active. Well, they were active. They couldn’t go any further than the cord. We had to string wires down the hall. . . . And then, if they needed an X ray or something that couldn’t be done in the room, you couldn’t get on the elevator so you had to string them down the stairwells. It seemed that almost everything you wanted was on a different floor. We needed something battery-operated.’’

From Machines In Our Hearts.

The plug-in stimulator was more than an inconvenience, for by introducing the myocardial pacing wire, Lillehei and his associates had connected the hearts of their surgical patients to the 110-volt electrical system of the hospital. Everyone in the program knew that an electrical surge might send patients into ventricular fibrillation or that a power outage could leave them without pacemaker support. On October 31, 1957, an equipment failure at a large Twin Cities power plant caused an outage lasting nearly three hours in Minneapolis. The University hospital had auxiliary power in its surgical suites and recovery area, but not in patients’ rooms. None of his heart patients died—but Lillehei viewed the event as a warning. Lillehei…turned to Earl Bakken…a young engineer who owned a small medical electronics business called Medtronic and repaired and serviced equipment for the Department of Surgery.

Bakken…realized that he could simply build a stimulator that used transistors and small batteries. ‘‘It was kind of an interesting point in history,’’ he recalled—‘‘a joining of several technologies.’’ In constructing the external pulse generator, Bakken borrowed a circuit design for a metronome that he had noticed a few months earlier in an electronics magazine for hobbyists. It included two transistors. Invented a decade earlier, the transistor was just beginning to spread into general use in the mid-1950s. Hardly anyone had explored its applications in medical devices. Bakken used a nine-volt battery, housed the assemblage in an aluminum circuit box, and provided an on-off switch and control knobs for stimulus rate and amplitude.

At the electronics repair shop that he had founded with his brother-in-law in 1949, Bakken had customized many instruments for researchers at the University of Minnesota Medical School…When Bakken delivered the battery-powered external pulse generator to Walt Lillehei in January 1958, it seemed to the inventor another special order, nothing more. The pulse generator was hardly an aesthetic triumph, but it was small enough to hold in the hand and severed all connection between the patient’s heart and the hospital power system. Bakken’s business had no animal-testing facility, so he assumed that the surgeons would test the device by pacing laboratory dogs. They did ‘‘a few dogs,’’ then Lillehei put the pacemaker into clinical use. When Bakken next visited the university, he was surprised to find that his crude prototype was managing the heartbeat of a child recovering from open-heart surgery.

The Bakken Museum. From wikipedia.

Russ Hobbie is retired from the University of Minnesota, and still lives in the area, so he is particularly familiar with Earl Bakken. He served on the board of the Bakken Museum, which is devoted to bioelectricity (my kind of museum). Russ say he ‘‘was impressed by Bakken's vision, energy, and desire to help people. The Bakken Museum has an extensive outreach program which does a lot of good things.’’ They recently posted a statement honoring their founder.

Medtronic is one of the largest medical device companies. I had a job interview there years ago, but I didn’t get the position. I came away impressed by the company, and wish I had bought stock.

Bakken is a member of the dwindling greatest generation; he was an airborne radar maintenance instructor during World War II. He had a long, full life, and we will miss him.

Below are a couple of videos about Earl Bakken. Enjoy!

The Bond Number

In graduate school, I did experiments on nerves submerged in saline. When dissecting or manipulating the tissue, I was amazed by the effect of surface tension compared to gravity; bubbles would stick to my forceps, and when I raised my scalpel out of the saline all kinds of stuff came along with it.

A dimensionless number describes this effect: the Bond number (sometimes called the Eötvös number). Several dimensionless numbers—such as the Reynolds number, the Peclet number, and the Lewis number—are mentioned in Intermediate Physics for Medicine and Biology. They indicate the relative importance of two physical mechanisms. Because they are dimensionless, their value does not depend on the units used. I find them useful.

The Bond number, Bo, is the ratio of the gravitational force mg (where m is the mass and g is the acceleration of gravity) to the force due to surface tension γL (where γ is the surface tension and L is some characteristic length such as the radius for a sphere), so Bo = mg/γL. If the Bond number is much greater than one, gravity dominates and surface tension is relatively insignificant. If the Bond number is much less than one, surface tension dominates and gravity hardly matters (like during my nerve experiments). When it’s close to one, both forces are similar.

The Bond number can help answer questions such as: Can animals stand on water? Insects can but people can’t. Why? Consider how the Bond number scales with size. An animal’s mass is equal to its density ρ times its volume, which varies as L³. In that case, the Bond number has an L³ in the numerator and an L in the denominator, so it scales as L².

If an animal is large enough, gravity wins and it sinks.

Let's estimate the size of an animal when the Bond number is one.

Take g = 9.8 m/s², ρ = 1000 kg/m³, and γ = 0.07 N/m (for water on earth). We find that L = 3 mm. For an insect, the good news is that it can stand on water. The bad news is that surface tension holds it in place so it can hardly move. As Steven Vogel says in Life in Moving Fluids: “Staying up is easy, but getting around is awkward.”

The Bond number is also useful for studying capillary action. Water will climb up the walls of a tube because of cohesion between the wall and the fluid. Technically, this effect depends on the nature of the surface as measured by its contact angle; you can coat a surface with a substance that repels water so that water climbs down the tube, but we will ignore all that and assume the contact angle is so small that the water “wets” the surface and cohesion is the same as surface tension. The gravitational force of the climbing water is gρπR²H, where R is the tube radius and H is the height that the water climbs. The surface tension force is γ times the circumference of the tube, 2πR. The Bond number becomes gρRH/2γ. We expect water to rise until gravity and surface tension are in balance, or until about Bo = 1. The height is then H = 2γ/gρR. For a 1 mm radius tube, the height is 14 mm, or roughly half an inch.

Can capillary action explain the ascent of sap in trees? The tubes in a tree's xylem have a radius of about 20 microns. In that case, water will rise about 0.6 meters. That’s about two feet, which doesn’t explain how water gets up a 100-m giant redwood. Suffice to say, the trunk of a redwood tree does not act as a giant wick, sucking water up its trunk by capillary action.

Wilfrid Noel Bond, from Wikipedia.

The Bond number is named after the English physicist Wilfrid Noel Bond (1897-1937). He studied fluid dynamics, including viscosity and surface tension. He died tragically early at age 39.

If you want to learn more about the Bond number and other dimensionless numbers, see Vogel’s 1998 article in Physics Today about “Exposing Life’s Limits with Dimensionless Numbers.”

A Trick to Generate Exam Problems

Intermediate Physics for Medicine and Biology.

When teaching a class based on Intermediate Physics for Medicine and Biology, instructors need to write problems for their exams. My goal in this post is to explain a trick for creating good exam problems. 

One of my favorite homework problems in IPMB is from Chapter 4.

Problem 37. The goal of this problem is to estimate how large a cell living in an oxygenated medium can be before it is limited by oxygen transport. Assume the extracellular space is well stirred with uniform oxygen concentration C₀. The cell is a sphere of radius R. Inside the cell oxygen is consumed at a rate Q molecule m⁻³ s⁻¹. The diffusion constant for oxygen in the cell is D.

(a) Calculate the concentration of oxygen in the cell in the steady state.

(b) Assume that if the cell is to survive the oxygen concentration at the center of the cell cannot become negative. Use this constraint to estimate the maximum size of the cell.

(c) Calculate the maximum size of a cell for C₀ = 8 mol m⁻³, D = 2 x 10⁻⁹ m² s⁻¹, Q = 0.1 mol m⁻³ s⁻¹. (This value of Q is typical of protozoa; the value of C₀ is for air and is roughly the same as the oxygen concentration in blood.)

Homework problems for Chapter 4 in
Intermediate Physics for Medicine and Biology.

I usually work this problem in class. Not only do students practice solving the steady-state diffusion equation, but also they estimate the maximum size of a cell from some basic properties of oxygen. In the Solution Manual—available to instructors only (email us)—we explain the purpose of each problem in a preamble. Here is what the solution manual says about Problem 37:

This important “toy model” considers the maximum size of a spherical cell before its core dies from lack of oxygen. One goal of biological physics is to show how physics constrains evolution. In this case, the physics of diffusion limits how large an animal can be before needing a circulatory system to move oxygen around.

How do you create an exam problem on this subject? Here's the trick: Do Problem 37 in class and then put a question on the exam identical to Problem 37 except “sphere” is replaced by “cylinder”. The problem is only slightly changed; just enough to determine if the student is solving the problem from first principles or merely memorizing. In addition, nerve and muscle fibers are cylindrical, so the revised problem may provide an even better model for those cells. Depending on the mathematical abilities of your students, you may need to provide students with the Laplacian in cylindrical coordinates. (If the exam is open book then they can find the Laplacian in Appendix L).

Here’s a second example: Chapter 1 considers viscous flow in a tube; Poiseuille flow. On the exam, ask the student to analyze viscous flow between two stationary plates.

Section 1.17

Problem 36 ½. Consider fluid flow between two stationary plates driven by a pressure gradient. The pressure varies in the x direction with constant gradient dp/dx, the plates are located at y = +L and y = -L, and the system is uniform in the z direction with width H. The fluid has viscosity η.

(a) Draw a picture the geometry.

(b) Consider a rectangular box of fluid centered at the origin and derive a differential equation like Eq. 1.35 governing the velocity v_x(y).

(c) Solve this differential equation to determine v_x(y), analogous to Eq. 1.37. Assume a no-slip boundary condition at the surface of each plate. Plot v_x(y) versus y.

(d) Integrate the volume fluence and find the total flow i. How does i depend on the plate separation, 2L? How does this compare with the case of flow in a tube?

An interesting feature of this example is that i depends on the third power of L, whereas for a tube it depends on the fourth power of the radius. Encourage the student to wonder why.

Third example: A problem in Chapter 7 compares three different functions describing the strength-duration curve for electrical stimulation. On your exam, have the students analyze a fourth case.

Section 7.10

Problem 46 ½. Problem 46 analyzes three possible functions that could describe the strength-duration curve, relating the threshold current strength required for neural excitation, i, to the stimulus pulse duration, t. Consider the function i = A/tan^-1(t/B). Derive expressions for the rheobase i_R and chronaxie t_C in terms of A and B. Write the function in the form used in Problem 46. Plot i versus t.

And still more: Problem 32 in Chapter 8 examines magnetic stimulation of a nerve axon using an applied electric field E_i(x) = E₀ a²/(x² + a²). Give a similar problem on your exam but use a different electric field, such as E_i(x) = E₀ exp(-x²/a²).

And yet another: Chapter 10 examines the onset of cardiac fibrillation and chaos. The action potential duration APD is related to the diastolic interval (time from the end of the previous action potential to the start of the following one) DI by the restitution curve. Have the student repeat Problem 41 but using a different restitution curve: APD_i+1 = 300 DI_i/(DI_i + 100).

Final example: Problem 36 in Chapter 9 asks the student to calculate the electrical potential inside and outside a spherical cell in the presence of a uniform electric field (Figure 9.19). On your exam, make the sphere into a cylinder.

I think you get the point. On an exam, repeat one the of homework problems in IPMB, but with a twist. Change the problem slightly, using a new function or a modified geometry. You will be able to test the knowledge and understanding of the student without springing any big surprises on the exam. Many problems in IPMB that could be modified in this way.

Warning: This trick doesn’t always work. For instance, in Chapter 1 if you try to analyze fluid flow perpendicular to a stationary object, you run into difficulties when you change the sphere of Problem 46 into a cylinder. The cylindrical version of this problem has no solution! The lack of a solution for low Reynolds number flow around a cylinder is known as Stokes’ Paradox. In that case, you’re just going to have to think up your own exam question.

A Bidomain Model for the Extracellular Potential and Magnetic Field of Cardiac Tissue

My research notebooks from graduate school.

In graduate school, I worked with John Wikswo measuring the magnetic field of a nerve axon. We isolated a crayfish axon and threaded it through a wire-wound ferrite-core toroid immersed in saline. As the action currents propagated by, they produced a changing magnetic field that induced a signal in the toroid by Faraday induction. Ampere’s law tells us that the signal is proportional to the net current through the toroid, which is the sum of the intracellular current and the fraction of the current in the saline that passes through the toroid, called the return current.

For my PhD dissertation, Wikswo had me make similar measurements on strands of cardiac tissue, such as a papillary muscle. The instrumentation was the same as for the nerve, but the interpretation was different. Now the signal had three sources: the intracellular current, the return current in the saline, and extracellular current passing through the interstitial space within the muscle called the “interstitial return current.” Initially neither Wikswo nor I knew how to calculate the interstitial return current, so we were not sure how to interpret our results. As I planned these experiments, I recorded my thoughts in my research notebook. The July 26, 1984 entry stressed that “Understanding this point [the role of interstitial return currents] will be central to my research and deserves much thought.”

Excerpt from the July 26, 1984 entry in my Notebook 8, page 64.

When working on nerves, I had studied articles by Robert Plonsey and John Clark, in which they calculated the extracellular potential in the saline from the measured voltage across the axon’s membrane: the transmembrane potential. I was impressed by this calculation, which involved Fourier transforms and Bessel functions (see Chapter 7, Problem 30, in Intermediate Physics for Medicine and Biology). I had used their result to calculate the magnetic field around an axon (see Chapter 8, Problem 16 in IPMB), so I set out to extend their analysis again to include interstitial return currents.

Page 1 of Notebook 9, from Sept 13, 1984.

The key was to use the then-new bidomain model, which accounts for currents in both the intracellular and interstitial spaces. The crucial advance came in September 1984 after I read a copy of Les Tung’s PhD dissertation that Wikswo had loaned me. After four days of intense work, I had solved the problem. My results looked a lot like those of Clark and Plonsey, except for a few strategically placed additional factors and extra terms.

Excerpt from Notebook 9, page 13, the Sept 16, 1984 entry.

First page of Roth and Wikswo (1986).

Wikswo and I published these results as a brief communication in the IEEE Transactions on Biomedical Engineering.

Roth, B. J. and J. P. Wikswo, Jr., 1986, A bidomain model for the extracellular potential and magnetic field of cardiac tissue. IEEE Trans. Biomed. Eng., 33:467-469.

Abstract—In this brief communication, a bidomain volume conductor model is developed to represent cardiac muscle strands, enabling the magnetic field and extracellular potential to be calculated from the cardiac transmembrane potential. The model accounts for all action currents, including the interstitial current between the cardiac cells, and thereby allows quantitative interpretation of magnetic measurements of cardiac muscle.

Rather than explain the calculation in all its gory detail, I will ask you to solve it in a new homework problem.

Section 7.9

Problem 31½. A cylindrical strand of cardiac tissue, of radius a, is immersed in a saline bath. Cardiac tissue is a bidomain with anisotropic intracellular and interstitial conductivities σ_ir, σ_iz, σ_or, and σ_oz, and saline is a monodomain volume conductor with isotropic conductivity σ_e. The intracellular and interstitial potentials are V_i and V_o, and the saline potential is V_e.

a) Write the bidomain equations, Eqs. 7.44a and 7.44b, for V_i and V_o in cylindrical coordinates (r,z). Add the two equations.

b) Assume V_i = σ_iz/(σ_iz+σ_oz) [A I₀(kλr) + (σ_oz/σ_iz) V_m] sin(kz) and V_o = σ_iz/(σ_iz+σ_oz) [A I₀(kλr) - V_m] sin(kz) where λ² = (σ_iz+σ_oz)/(σ_ir+σ_or). Verify that V_i - V_o equals the transmembrane potential V_m sin(kz). Show that V_i and V_o obey the equation derived in part a). I₀(x) is the modified Bessel function of the first kind of order zero, which obeys the modified Bessel equation d²y/dx² + (1/x) dy/dx = y. Assume V_m is independent of r.

c) Write Laplace’s equation (Eq. 7.38) in cylindrical coordinates. Assume V_e = B K₀(kr) sin(kz). Show that V_e satisfies Laplace’s equation. K₀(x) is the modified Bessel function of the second kind of order zero, which obeys the modified Bessel equation.

d) At r = a, the boundary conditions are V_o = V_e and σ_ir∂V_i/∂r + σ_or∂V_o/∂r = σ_e∂V_e/∂r. Determine A and B. You may need the Bessel function identities dI₀/dx = I₁ and dK₀/dx = - K₁, where I₁(x) and K₁(x) are modified Bessel functions of order one.

In the problem above, I assumed the potentials vary sinusoidally with z, but any waveform can be expressed as a superposition of sines and cosines (Fourier analysis) so this is not as restrictive as it seems.

In part b), I assumed the transmembrane potential was not a function of r. There is little data supporting this assumption, but I was stuck without it. Another assumption I could have used was equal anisotropy ratios, but I didn’t want to do that (and initially I didn’t realize it provided an alternative path to the solution).

The calculation of the magnetic field is not included in the new problem; it requires differentiating V_i, V_o, and V_e to find the current density, and then integrating the current to find the magnetic field via Ampere’s law. You can find the details in our IEEE TBME communication.

Some of you might be thinking “this is a nice homework problem, but how did you get those weird expressions for the intracellular and interstitial potentials used in part b)”? Our article gives some insight, and my notebook provides more. I started with Clark and Plonsey’s result, used ideas from Tung’s dissertation, and then played with the math (trial and error) until I had a solution that obeyed the bidomain equations. Some might call that a strange way to do science, but it worked for me.

I was very proud of this calculation (and still am). It played a role in the development of the bidomain model, which is now considered the state-of-the-art model for simulating the heart during defibrillation.

Wikswo and I carried out experiments on guinea pig papillary muscles to test the calculation, but the cardiac data was not as clean and definitive as our nerve data. We published it as a chapter in Cell Interactions and Gap Junctions (1989). The cardiac work made up most of my PhD dissertation. Vanderbilt let me include our three-page IEEE TBME communication as an appendix. It’s the most important three pages in the dissertation.


Coda: While browsing through my old research notebooks, I found this gem passed from Prof. Wikswo to his earnest but naive graduate student, who dutifully wrote it down in his research notebook for posterity.

Excerpt from Notebook 10, Page 62.

Steven Strogatz Lectures on Youtube

Nonlinear Dynamics and Chaos.

Previously (here, here, and here), I’ve written about Steven Strogatz, Professor of Applied Mathematics at Cornell University. Strogatz wrote one of my favorite textbooks: Nonlinear Dynamics and Chaos. Russ Hobbie and I cite it in Chapter 10 of Intermediate Physics for Medicine and Biology.

Nowadays students rarely read textbooks; they prefer watching videos. Well, I have good news. Strogatz taught a course based on his book, and his lectures are posted on YouTube. You can learn chaos straight from the horse’s mouth. You better get started: there are over 24 hours of video (all embedded below).

The 2nd Edition of Nonlinear Dynamics and Chaos.

Strogatz is an enormously successful mathematician. According to Google Scholar, his 1998 article with Duncan Watts—“Collective Dynamics of ‘Small-World’ Networks” (Nature, Volume 393, Pages 440-442)—has been cited over 35,000 times! His textbook has over ten thousand citations. (To put this in perspective, IPMB has 392.) He won the Lewis Thomas Prize for Writing about Science, tweets at @stevenstrogatz, and is buddies with M*A*S*H star and science communicator Alan Alda. In IPMB, Russ and I cite the first edition of Nonlinear Dynamics and Chaos, but Strogatz published a second edition in 2015.

Enjoy!

 

1. Introduction and Overview

2. One Dimensional Systems

3. Overdamped Bead on a Rotating Hoop

4. Model of Insect Outbreak

5. Two Dimensional Nonlinear Systems

6. Two Dimensional Nonlinear Systems Fixed Points

7. Conservative Systems

8. Index Theory and Introduction to Limit Cycles

9. Testing for Closed Orbits

10. Van der Pol Oscillator

11. Averaging Theory for Weakly Nonlinear Oscillators

12. Bifurcations in Two Dimensional Systems

13. Hopf Bifurcations in Aeroelastic Instabilities and Chemical Oscillators

14. Global Bifurcations of Cycles

 15. Chaotic Waterwheel

16. Waterwheel Equations and Lorenz Equations

17. Chaos in the Lorenz Equations

18. Strange Attractor for the Lorenz Equations

19. One Dimensional Maps

20. Universal Aspects of Period Doubling

21. Feigenbaum’s Renormalization Analysis of Period Doubling

22. Renormalization: Function Space and a Hands-on Calculation

23. Fractals and the Geometry of Strange Attractors

24. Henon Map

25. Using Chaos to Send Secret Messages

Quick Calculus

In Intermediate Physics for Medicine and Biology, Russ Hobbie and I assume the reader knows calculus. Some readers, however, have weak or rusty math skills. Is there an easy way to learn what is needed?

Quick Calculus.

Yes! Quick Calculus is a self-teaching guide written by Daniel Klepner and Norman Ramsey. Their preface states:

Before you plunge into Quick Calculus, perhaps we ought to tell you what it is supposed to do. Quick Calculus should teach you the elementary techniques of differential and integral calculus with a minimum of wasted effort on your part; it is designed for you to study by yourself. Since the best way for anyone to learn calculus is to work problems, we have included many problems in this book. You will always see the solution to your problem as soon as you have finished it, and what you do next will depend on your answer. A correct answer generally sends you to new material, while an incorrect answer sends you to further explanations and perhaps another problem.

The book covers nearly all the calculus needed in IPMB.

• Chapter One reviews functions and graphs, emphasizing trigonometry, exponentials, and logarithms.
• Chapter Two discusses differentiation—including the product rule and the chain rule—and maximum/minimum problems.
• Chapter Three analyzes integration, both definite and indefinite, and covers techniques such as change of variable, integration by parts, and multiple integrals.
• Chapter Four summarizes all the results in a few pages.

Math Books Useful for IPMB.

The only calculus in IPMB that Quick Calculus doesn’t teach is vector calculus; for that you should consult Div, Grad, Curl and All That. Used Math covers more ground than Quick Calculus, but it’s a handbook rather than a self-teaching guide.

Quick Calculus has several virtues. It is clearly written, it emphasizes understanding math visually with lots of plots, and it focuses on utilitarian techniques without distracting rigor. If you want to understand math at a fundamental level, you should take a real calculus class. If you want to brush up on what's needed to get through IPMB, use Quick Calculus.

One disadvantage is that Quick Calculus is old. The second edition—the most recent one I am aware of—was published in 1985. It might be difficult to purchase, although Amazon seems to have copies for sale. The authors make quaint comments about “readers who have an electronic calculator,” as opposed to slide rules I suppose. I also found several typos, which might frustrate readers using the book for self-study.

A sample from Quick Calculus.

The format is unusual. The text is divided into approximately half-page “frames,” and the reader is guided from one frame to the next. Someone should put this book online, because it would lend itself to an interactive online format. Rather than explain how the book is organized, I’ve taken Section 1.17 of IPMB and rewritten it in the style of Quick Calculus (see below). In my opinion, if all of Intermediate Physics for Medicine and Biology were organized like this it would be tedious. What do you think?