A dimensionless number describes this effect: the Bond number (sometimes called the Eötvös number). Several dimensionless numbers—such as the Reynolds number, the Peclet number, and the Lewis number—are mentioned in Intermediate Physics for Medicine and Biology. They indicate the relative importance of two physical mechanisms. Because they are dimensionless, their value does not depend on the units used. I find them useful.
The Bond number, Bo, is the ratio of the gravitational force mg (where m is the mass and g is the acceleration of gravity) to the force due to surface tension γL (where γ is the surface tension and L is some characteristic length such as the radius for a sphere), so Bo = mg/γL. If the Bond number is much greater than one, gravity dominates and surface tension is relatively insignificant. If the Bond number is much less than one, surface tension dominates and gravity hardly matters (like during my nerve experiments). When it’s close to one, both forces are similar.
The Bond number can help answer questions such as: Can animals stand on water? Insects can but people can’t. Why? Consider how the Bond number scales with size. An animal’s mass is equal to its density ρ times its volume, which varies as L3. In that case, the Bond number has an L3 in the numerator and an L in the denominator, so it scales as L2.
If an animal is large enough, gravity wins and it sinks.
Let's estimate the size of an animal when the Bond number is one.
Take g = 9.8 m/s2, ρ = 1000 kg/m3, and γ = 0.07 N/m (for water on earth). We find that L = 3 mm. For an insect, the good news is that it can stand on water. The bad news is that surface tension holds it in place so it can hardly move. As Steven Vogel says in Life in Moving Fluids: “Staying up is easy, but getting around is awkward.”
The Bond number is also useful for studying capillary action. Water will climb up the walls of a tube because of cohesion between the wall and the fluid. Technically, this effect depends on the nature of the surface as measured by its contact angle; you can coat a surface with a substance that repels water so that water climbs down the tube, but we will ignore all that and assume the contact angle is so small that the water “wets” the surface and cohesion is the same as surface tension. The gravitational force of the climbing water is gρπR2H, where R is the tube radius and H is the height that the water climbs. The surface tension force is γ times the circumference of the tube, 2πR. The Bond number becomes gρRH/2γ. We expect water to rise until gravity and surface tension are in balance, or until about Bo = 1. The height is then H = 2γ/gρR. For a 1 mm radius tube, the height is 14 mm, or roughly half an inch.
Can capillary action explain the ascent of sap in trees? The tubes in a tree's xylem have a radius of about 20 microns. In that case, water will rise about 0.6 meters. That’s about two feet, which doesn’t explain how water gets up a 100-m giant redwood. Suffice to say, the trunk of a redwood tree does not act as a giant wick, sucking water up its trunk by capillary action.
 |
| Wilfrid Noel Bond, from Wikipedia. |
If you want to learn more about the Bond number and other dimensionless numbers, see Vogel’s 1998 article in Physics Today about “Exposing Life’s Limits with Dimensionless Numbers.”
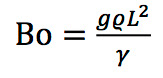




In "Life's Devices," Vogel refers to the inverse of the Bond number as the Jesus number, since it's the dimensionless ratio for the feasibility of walking on water!
ReplyDeletehttps://books.google.com/books?id=i7R5DyPQ13sC&pg=PA70&lpg=PA70#v=onepage&q&f=false
LOL
ReplyDelete