Otto Schmitt and the Bidomain Model

In Chapter 7 of Intermediate Physics for Medicine and Biology, Russ Hobbie and I discuss the bidomain model.

Myocardial cells are typically about 10 μm in diameter and 100 μm long. They have the added complication that they are connected to one another by gap junctions… This allows currents to flow directly from one cell to another without flowing in the extracellular medium. The bidomain (two-domain) model is often used to model this situation… It considers a region, small compared to the size of the heart, that contains many cells and their surrounding extracellular fluid. It simplifies the problem by assuming that each small volume element contains two domains, intracellular and extracellular.

The bidomain model has become the state-of-the-art representation of the electrical properties of cardiac tissue, and much of my research was focused on it. Les Tung’s 1979 PhD dissertation was one of the first publications to use the model (“A Bi-Domain Model for Describing Ischemic Myocardial DC Potentials,” Massachusetts Institute of Technology). I read his dissertation in graduate school and it had a huge impact on my research. Tung writes

The bidomain structure developed here is a detailed, quantitative realization of the concept of interpenetrating domains, described qualitatively by Schmitt (1969).

At about the same time, David Geselowitz and his student Tom Miller developed a similar model. In a 1983 paper (“A Bidomain Model for Anisotropic Cardiac Tissue,” Annals of Biomedical Engineering, Volume 11, Pages 191–206), they also cite the same source.

Schmitt (20) introduced the concept of “interpenetrating domains” based on a consideration of the electrical properties of a region containing many cells. He proposed that each point in the muscle be represented by an intracellular resistivity “representing cytoplasmic impedance of a neighborhood of like cells on a volume normalized basis,” and by a similar extracellular resistivity. The two would be connected at each point by a distributed nonlinear admittivity simulating active cell membrane.

In 1984, Robert Plonsey and Roger Barr published an early paper about the bidomain model (“Current Flow Patterns in Two-Dimensional Anisotropic Bisyncytia with Normal and Extreme Conductivities,” Biophysical Journal, Volume 45, Pages 557–571). They wrote 

Because the viewpoint is global rather than cellular (discrete) it is convenient to consider both intracellular space and interstitial space to be continuous and described by the same coordinates (both spaces are necessarily congruent, or, as described by Schmitt (2), “interpenetrating domains”).

All three publications cite the same book chapter by Otto Schmitt titled “Biological Information Processing Using the Concept of Interpenetrating Domains” (in Information Processing in The Nervous System, Leibovic, K. N., editor, Springer, Berlin, Pages 325–331). I decided that if this chapter is the true source of the bidomain concept, then I should read it (or reread it, as I remember looking at it decades ago). The interesting feature about the chapter is not what’s in it, but what isn’t. Schmitt never uses these words: bidomain, cardiac, heart, myocardium, syncytium, gap junction, or cable. Instead, the chapter focuses entirely on the nervous system, and never even hints at cardiovascular applications. So, what did Schmitt write that was so influential?

Let us introduce the notion of a local regional electrical vector impedivity representing cytoplasmic impedance of a neighborhood of like cells on a volume normalized basis and similarly represent regional interstitial fluid as an external impedivity with similar normalization and vectorial properties. Connect these two at every point by a distributed, scalar, nonlinear admittivity, simulating typical active cell membrane.

Schmitt then presents a more visual description of his idea.

If there is difficulty in comprehending this triple interpenetration of two impedivity and one admittivity domains, think of the following homely illustration. Imagine a three dimensional cubic fly screen of resistance wire as the first impedivity. Notice that another identical screen of perhaps different conductivity could be fitted completely within the first fly screen without touching it. A moderately conductive fluid poured into the fly screen system would, for all practical purposes, connect the two screens everywhere but only in a very limited neighborhood around each paired mesh cell would this conductivity be important.

Schmitt called this the interpenetrating domain model, but nowadays we call it the bidomain model (or sometimes, the bisyncytial model). Ironically, this idea is rarely used to model the nervous system, which was what Schmitt had in mind. It’s most applicable to syncytial tissues: when the cytoplasm of an individual cell is coupled to neighboring cells through gap junctions. Without such intercellular channels, the intracellular domain is not coupled like a “fly screen” but rather consists of uncoupled individual cells. Cardiac muscle is the classic example of a tissue in which all the cells are coupled via gap junctions, so it acts like a syncytium. 

Interestingly, the fly screen analogy looks similar to this bidomain resistor illustration, versions of which I've used in many publications.

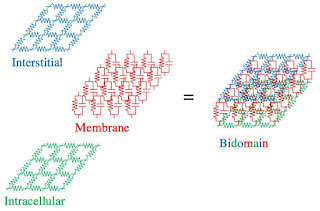The Bidomain Model (two interpenetrating domains).

I think it’s a stretch to say that Schmitt is the father of the bidomain model. Perhaps grandfather would better characterize his contribution. He didn’t derive a mathematical formulation of his idea. But he certainly conceived an intuitive picture of two coupled interpenetrating domains, and that influenced later work by Tung, Geselowitz, and Plonsey.

I’ll end with the abstract from a short biography of Otto Schmitt by Jon Harkness (Physics in Perspective, Volume 4, Pages 456-490, 2002), written four years after Schmitt’s death.

A Lifetime of Connections: Otto Herbert Schmitt, 1913–1998 

Jon M. Harkness

Otto H. Schmitt was born in St. Louis, Missouri, in 1913. As a youth, he displayed an affinity for electrical engineering but also pursued a wide range of other interests. He applied his multi-disciplinary talents as an undergraduate and graduate student at Washington University, where he worked in three departments: physics, zoology, and mathematics. For his doctoral research, Schmitt designed and built an electronic device to mimic the propagation of action potentials along nerve fibers. His most famous invention, now called the Schmitt trigger, arose from this early research. Schmitt spent most of his career at the University of Minnesota, where he did pioneering work in biophysics and bioengineering. He also worked at national and international levels to place biophysics and bioengineering on sound institutional footings. His years at Minnesota were interrupted by World War II. During that conflict—and the initial months of the Cold War to follow—Schmitt carried out defense-related research at the Airborne Instruments Laboratory in New York. Toward the end of his career at Minnesota, Schmitt coined the term biomimetics. He died in 1998.

Otto Schmitt discussing his work during World War II.

https://www.youtube.com/watch?v=lMCJG2C2_CY

Numerical Recipes is Online

Numerical Recipes,
by Press, Teukolsky, Vetterling, and Flannery.

In Intermediate Physics for Medicine and Biology, Russ Hobbie and I often refer to Numerical Recipes: The Art of Scientific Computing, by William Press, Saul Teukolsky, William Vetterling, and Brian Flannery. We usually cite the second edition of the book with programs written in C (1995), but the copy on my bookshelf is the second edition using Fortran 77 (1992). For those of you who don’t own a copy of this wonderful book, did you know you can read it online?

The address of the Numerical Recipes website is easy to remember: numerical.recipes. There you will find free copies of the second editions of Numerical Recipes for Fortran 77, Fortran 90, C, and C++ (2002). If you want easy, quick access to the third edition (2007), you will have to pay a fee. But if you are willing to put up with brief delays and annoying messages (which the authors call “nags”), you also can read the third edition for free.

The text below is from the Preface to the third edition.

“I was just going to say, when I was interrupted...” begins Oliver Wendell Holmes in the second series of his famous essays, The Autocrat of the Breakfast Table. The interruption referred to was a gap of 25 years. In our case, as the autocrats of Numerical Recipes, the gap between our second and third editions has been “only” 15 years. Scientific computing has changed enormously in that time.

The first edition of Numerical Recipes was roughly coincident with the first commercial success of the personal computer. The second edition came at about the time that the Internet, as we know it today, was created. Now, as we launch the third edition, the practice of science and engineering, and thus scientific computing, has been profoundly altered by the mature Internet and Web. It is no longer difficult to find somebody’s algorithm, and usually free code, for almost any conceivable scientific application. The critical questions have instead become, “How does it work?” and “Is it any good?” Correspondingly, the second edition of Numerical Recipes has come to be valued more and more for its text explanations, concise mathematical derivations, critical judgments, and advice, and less for its code implementations per se.

Recognizing the change, we have expanded and improved the text in many places in this edition and added many completely new sections. We seriously considered leaving the code out entirely, or making it available only on the Web. However, in the end, we decided that without code, it wouldn’t be Numerical Recipes. That is, without code you, the reader, could never know whether our advice was in fact honest, implementable, and practical. Many discussions of algorithms in the literature and on the Web omit crucial details that can only be uncovered by actually coding (our job) or reading compilable code (your job). Also, we needed actual code to teach and illustrate the large number of lessons about object-oriented programming that are implicit and explicit in this edition.

Russ and I cited Numerical Recipes in IPMB when we discussed integration, least squares fitting, random number generators, partial differential equations, the fast Fourier transform, aliasing, the correlation function, the power spectral density, and bilinear interpolation. Over the years, in my own research I have consulted the book about other topics, including solving systems of linear equations, evaluation of special functions, and computational analysis of eigensystems.

I highly recommend Numerical Recipes to anyone doing numerical computing. I found the book to be indispensable.

The Annotated Hodgkin & Huxley: A Readers Guide

The Annotated Hodgkin & Huxley,
by Indira Raman and David Ferster.

I have always loved the classic set of five papers published by Hodgkin and Huxley in the Journal of Physiology. I often assigned the best of these, the fifth paper, when I taught my Biological Physics class. But reading the original papers can be a challenge. I was therefore delighted to discover The Annotated Hodgkin & Huxley: A Readers Guide, by Indira Raman and David Ferster. In their introduction, they write

After nearly seventy years, Alan Hodgkin and Andrew Huxley’s 1952 papers on the mechanisms underlying the action potential seem more and more like the Shakespeare plays of neurophysiology, works of astounding beauty that become less accessible to each successive generation of scientists. Everyone knows the basic plot (the squid dies at the beginning), but with their upside-down and backwards graphs and records, unfamiliar terminology and techniques, now arcane scientific asides, and complex mathematical underpinnings, the papers become a major effort to read closely without guidance. It is our goal to provide such guidance, by translating graphs and terminology into the modern idiom, explaining the methods and underlying theory, and providing historical perspective on the events that led up to the experiments described. By doing so, we hope to bring the pleasure of reading these extraordinary papers to any physiologist inclined to read them.

Raman and Ferster then give seven reasons to be so inclined.

• “The sheer pleasure of an exciting scientific saga...” 
• “Coming to know the electrical principles that govern the operation of neurons...” 
• “To see firsthand what it is like to be at a scientific frontier...” 
• “The series of papers provide an exemplary…illustration of the scientific method at its best...” 
• “To understand the purpose and power of quantification and computation in science...” 
• “The papers teach us that rigorous science does not require the elimination of error and artifact,”
• “To develop a sense of one’s place in history.”

After a brief chapter about the historical background, the fun really begins. Each of the five papers is presented verbatim on even-numbered pages, with annotations (notes, redrawn figures, explanations, comments) on facing odd-numbered pages. 

One annoying problem with the original papers is that Hodgkin and Huxley defined the transmembrane potential differently than everyone else; they took resting potential to be zero and denote depolarization as negative. Raman and Ferster have redrawn all the figures using the modern definition; rest is −65 mV and depolarization is positive. With this change, the plots of the m, h, and n gates (which control the opening and closing of the sodium and potassium channels) versus transmembrane potential look the same as they do in Fig. 6.37 of Intermediate Physics for Medicine and Biology. I sometimes wish I could take a time machine, go back to 1952, and say “Hey Al! Hey Andy! Don’t use that silly convention for specifying the transmembrane potential. It will be a blemish your otherwise flawless series of papers.”

One of my favorite annotations is in response to Hodgkin and Huxley’s sentence “the equations derived in Part II of this paper [the fifth article in the series] predict with fair accuracy many of the electrical properties of the squid giant axon.” Raman and Ferster write “This may be the greatest understatement of the entire series of five papers.” I would say it’s one of the greatest understatements in all of science.

The final annotation follows Hodgkin and Huxley’s final sentence of their fifth paper: “it is concluded that the responses of an isolated giant axon of Loligo to electrical stimuli are due to reversible alterations in sodium and potassium permeability arising from changes in membrane potential.” Raman and Ferster add “H&H end their tour de force with a mild but precise statement that electrical excitability in the squid giant axon results from voltage-gated conductances. The discoveries that underlie this simple conclusion, however, completely transformed the understanding of cellular excitability in particular and bioelectricity in general. As John W. Moore—a postdoc with Kenneth Cole in 1952—once quipped, it took the rest of the field about a decade to catch up.”

The appendices at the end of The Annotated Hodgkin & Huxley are useful, particularly Appendix Five about numerical methods for solving the Hodgkin & Huxley equations. Huxley performed his calculations on a mechanical calculator. Raman and Ferster write

The mechanical calculator Huxley used was a pre-war era Brunsviga Model 20… which is an adding machine with a few features that streamline the calculations. To multiply 1234 by 5678, for example, one must follow these steps:

• Enter 1234 on the sliding levers (on the machine’s curved face), one digit at a time. 
• Position the carriage (at the front of the machine) in the ones position. 
• Turn the crank eight (at the far right) times. 
• Slide the carriage to the tens position 
• Turn the crank seven times. 
• Slide the carriage to the hundreds position. 
• Turn the crank six times. 
• Slide the carriage to the thousands position. 
• Turn the crank five times.
  

Thus, 30 individual operations are required to multiply two four-digit numbers.

Andrew Huxley, you are my hero.

Happy 70th anniversary of the publication of these landmark papers. I’ll end with a quote about them from Raman and Ferster’s epilogue

The following decades saw tremendous advances in physiology that built directly on the discoveries of H&H. Ultimately, what began as a basic scientific inquiry in a fragile invertebrate with a fortuitously oversized axon would provide the basis for the development of a vast array of biomedical research fields. The studies that the H&H papers made possible would not only yield immeasurable insights into brain and muscle function but also identify, explain, and alleviate medical conditions as diverse as epilepsies, ataxias, myotonias, arrhythmias, and pain.

Teaching Dynamics to Biology Undergraduates: the UCLA Experience

The goal of Intermediate Physics for Medicine and Biology, and the goal of this blog, is to explore the interface between physics, medicine, and biology. But understanding physics, and in particular the physics used in IPMB, requires calculus. In fact, Russ Hobbie and I state in the preface of IPMB that “calculus is used without apology.” Unfortunately, many biology and premed students don’t know much calculus. In fact, their general math skills are often weak; even algebra can challenge them. How can students learn enough calculus to make sense of IPMB?

A team from UCLA has developed a new way to teach calculus to students of the life sciences. The group is led by Alan Garfinkel, who appears in IPMB when Russ and I discuss the response of cardiac tissue to repetitive electrical stimulation (see Chapter 10, Section 12). An article describing the new class they’ve developed was published recently in the Bulletin of Mathematical Biology (Volume 84, Article Number 43, 2022).

There is a growing realization that traditional “Calculus for Life Sciences” courses do not show their applicability to the Life Sciences and discourage student interest. There have been calls from the AAAS, the Howard Hughes Medical Institute, the NSF, and the American Association of Medical Colleges for a new kind of math course for biology students, that would focus on dynamics and modeling, to understand positive and negative feedback relations, in the context of important biological applications, not incidental “examples.” We designed a new course, LS 30, based on the idea of modeling biological relations as dynamical systems, and then visualizing the dynamical system as a vector field, assigning “change vectors” to every point in a state space. The resulting course, now being given to approximately 1400 students/year at UCLA, has greatly improved student perceptions toward math in biology, reduced minority performance gaps, and increased students’ subsequent grades in physics and chemistry courses. This new course can be customized easily for a broad range of institutions. All course materials, including lecture plans, labs, homeworks and exams, are available from the authors; supporting videos are posted online.

Sharks and tuna, the predator-prey problem,
from Garfinkel et al.,
Bulletin of Mathematical Biology,
84:43, 2022.

This course approaches calculus from the point of view of modeling. Its first example develops a pair of coupled differential equations (only it doesn’t use such fancy words and concepts) to look at interacting populations of sharks and tuna; the classical predator-prey problem analyzed as a homework problem in Chapter 2 of IPMB. Instead of focusing on equations, this class makes liberal use of state space plots, vector field illustrations, and simple numerical analysis. The approach reminds me of that adopted by Abraham and Shaw in their delightful set of books Dynamics: The Geometry of Behavior, which I have discussed before in this blog. The UCLA course uses the textbook Modeling Life: The Mathematics of Biological Systems, which I haven’t read yet but is definitely on my list of books to read.

My favorite sentence from the article appears when it discusses how the derivative and integral are related through the fundamental theorem of calculus.

We are happy when our students can explain the relation between the COVID-19 “New Cases per day” graph and the “total cases” graph.

If you want to learn more, read the article. It’s published open access, so anyone can find it online. You can even steal its illustrations (like I did with its shark-tuna picture above).

I’ll end by quoting again from Garfinkel et al.’s article, when they discuss the difference between their course and a traditional calculus class. If you replace the words “calculus” and “math” by “physics” in this paragraph, you get a pretty good description of the approach Russ and I take in Intermediate Physics for Medicine and Biology.

The course that we developed has a number of key structural and pedagogical differences from the traditional “freshman calculus” or “calculus for life sciences” classes that have been offered at UCLA and at many other universities. For one, as described above, our class focuses heavily on biological themes that resonate deeply with life science students in the class. Topics like modeling ecological systems, the dynamics of pandemics like COVID-19, human physiology and cellular responses are of great interest to life science students. We should emphasize that these examples are not simply a form of window dressing meant to make a particular set of mathematical approaches palatable to students. Rather, the class is structured around the idea that, as biologists, we are naturally interested in understanding these kinds of systems. In order to do that, we need to develop a mathematical framework for making, simulating and analyzing dynamical models. Using these biological systems not purely as examples, but rather as the core motivation for studying mathematical concepts, provides an intellectual framework that deeply interests and engages life science students.

 

Introduction to state variables and state space. Video 1.1 featuring Alan Garfinkel.

https://www.youtube.com/watch?v=yZWG0ALL3mI

Defining vectors in higher dimensions. Video 1.2 featuring Alan Garfinkel.

https://www.youtube.com/watch?v=2Rjk0O3yWc8

The Emperor of All Maladies: A Biography of Cancer

One topic that appears over and over again throughout Intermediate Physics for Medicine and Biology is cancer. In Section 8.8, Russ Hobbie and I discuss using magnetic nanoparticles to heat a tumor. Section 9.10 describes the unproven hypothesis that nonionizing electromagnetic radiation can cause cancer. In Section 13.8, we analyze magnetic resonance guided high intensity focused ultrasound (MRgHIFUS), which has been proposed as a treatment for prostate cancer. Section 14.10 includes a discussion of how ultraviolet light can lead to skin cancer. One of the most common treatments for cancer, radiation therapy, is the subject of Section 16.10. Finally, in Section 17.10 we explain how positron emission tomography (PET) can assist in imaging metastatic cancer. Despite all this emphasis on cancer, Russ and I don’t really delve deeply into cancer biology. We should.

Last week, I attended a talk (remotely, via zoom) by my colleague and friend Steffan Puwal, who teaches physics at Oakland University. Steffan has a strong interest in cancer, and has compiled a reading list: https://sites.google.com/oakland.edu/cancer-reading. These books are generally not too technical but informative. I urge you to read some of them to fill that gap between physics and cancer biology.

The Emperor of All Maladies,
by Siddhartha Mukherjee.

Steffan says that the best of these books is The Emperor of All Maladies: A Biography of Cancer, by Siddhartha Mukherjee. Ken Burns has produced a television documentary based on this book. You can listen to the trailer at the bottom of this post. If you are looking for a more technical review paper, Steffan suggests “Hallmarks of Cancer: The Next Generation,” by Douglas Hanahan and Robert Weinberg (Cell, Volume 4, Pages 646–674, 2011). It’s open access, so you don’t need a subscription to read it. He also recommends the websites for the MD Anderson Cancer Center (https://www.mdanderson.org) and the Dana Farber Cancer Institute (https://www.dana-farber.org). 

Thanks, Steffan, for teaching me so much about cancer.

Cancer: The Emperor of All Maladies, Trailer with special introduction by Dr. Siddhartha Mukherjee.
 https://www.youtube.com/watch?v=L9lIsNkfQsM

 

Siddhartha Mukherjee, The Cancer Puzzle

 https://www.youtube.com/watch?v=vLH7e724TjA&t=178s

The Rest of the Story 3

Harry was born and raised in England and attended the best schools. After excelling at Summer Fields School, he won a King’s Scholarship to Eton College—the famous boarding school that produced twenty British Prime Ministers—where he won prizes in chemistry and physics. In 1906 he entered Trinity College at the University of Oxford, the oldest university in the English-speaking world, and four years later he graduated with his bachelor’s degree.

Next Harry went to the University of Manchester, where he worked with the famous physicist Ernest Rutherford. In just a few short years his research flourished and he made amazing discoveries. Rutherford recommended Harry for a faculty position back at Oxford. He might have taken the job, but after Archduke Franz Ferdinand of Austria was assassinated in Sarajevo in June 1914, the world blundered into World War I.

Like many English boys of his generation, Harry volunteered for the army. He joined the Royal Engineers, where he could use his technical skills as a telecommunications officer to support the war effort. Millions of English soldiers were sent to fight in France, where the war soon bogged down into trench warfare.

Page 2

First Lord of the Admiralty Winston Churchill devised a plan to break the deadlock. England would attack the Gallipoli peninsula in Turkey. If the navy could fight their way through the Dardanelles, they could take Constantinople, reach the Black Sea, unite with their ally Russia, and attack the “soft underbelly” of Europe. Harry was assigned to the expeditionary force for the Gallipoli campaign.

The plan was sound, but the execution failed; the navy could not force the narrows. The army landed on the tip of the peninsula and immediately settled into trench warfare like in France. There in Gallipoli, on August 10, 1915, a Turkish sniper shot and killed 27-year-old Second Lieutenant Henry Moseley—known as Harry to his boyhood friends.

Isaac Asimov wrote that Moseley’s demise “might well have been the most costly single death of the War to mankind.” Moseley’s research using x-rays to identify and order the elements in the periodic table by atomic number was revolutionary. He almost certainly would have received a Nobel Prize if that honor were awarded posthumously.

And now you know the REST OF THE STORY. Good Day!

-----------------------------------------------------------------------------------------------------

This blog entry was written in the style of Paul Harvey’s radio show “The Rest of the Story.” My February 5, 2016 and March 12, 2021 entries were also in this style. Homework Problem 3 in Chapter 16 of Intermediate Physics for Medicine and Biology explores Moseley’s work. Learn more about Henry Moseley in my March 16, 2012 blog entry.

Does a Nerve Axon Have an Inductance?

When I was measuring the magnetic field of a nerve axon in graduate school, I wondered if I should worry about a nerve’s inductance. Put another way, I asked if the electric field induced by the axon’s changing magnetic field is large enough to affect the propagation of the action potential.

Here is a new homework problem that will take you through the analysis that John Wikswo and I published in our paper “The Magnetic Field of a Single Axon” (Biophysical Journal, Volume 48, Pages 93–109, 1985). Not only does it answer the question about induction, but also it provides practice in back-of-the-envelope estimation. To learn more about biomagnetism and magnetic induction, see Chapter 8 of Intermediate Physics for Medicine and Biology.

Section 8.6

Problem 29½. Consider an action potential propagating down a nerve axon. An electric field E, having a rise time T and extended over a length L, is associated with the upstroke of the action potential.

(a) Use Ohm’s law to relate E to the current density J and the electrical conductivity σ. 

(b) Use Ampere’s law (Eq. 8.24, but ignore the displacement current) to estimate the magnetic field B from J and the permeability of free space, μ₀. To estimate the derivative, replace the curl operator with 1/L. 

(c) Use Faraday’s law (Eq. 8.22, ignoring the minus sign) to estimate the induced electric field E* from B. Replace the time derivative by 1/T. 

(d) Write your result as the dimensionless ratio E*/E. 

(e) Use σ = 0.1 S/m, μ₀ = 4 π × 10^-7 T m/A, L = 10 mm, and T = 1 ms, to calculate E*/E. 

(f) Check that the units in your calculation in part (e) are consistent with E*/E being dimensionless. 

(g) Draw a picture of the axon showing E, J, B, E*, and L. 

(h) What does your result in part (e) imply about the need to consider inductance when analyzing action potential propagation along a nerve axon.

For those of you who don’t have IPMB handy, Equation 8.24 (Ampere’s law, ignoring the displacement current) is

∇×B = μ₀ J

and Eq. 8.22 (Faraday’s law) is

∇×E = −∂B/∂t .

I’ll leave it to you to solve this problem. However, I’ll show you my picture for part (g).

Also, for part (e) I get a small value, on the order of ten parts per billion (10^-8). The induction of a nerve axon is negligible. We don't need an inductor when modeling a nerve axon.

How Far Can Bacteria Coast?

Random Walks in Biology,
by Howard Berg.

In last week’s blog post, I told you about the recent death of Howard Berg, author of Random Walks in Biology. This week, I present a new homework problem based on a topic from Berg’s book. When discussing the Reynolds number, a dimensionless number from fluid dynamics that is small when viscosity dominates inertia, Berg writes

The Reynolds number of the fish is very large, that of the bacterium is very small. The fish propels itself by accelerating water, the bacterium by using viscous shear. The fish knows a great deal about inertia, the bacterium knows nothing. In short, the two live in very different hydrodynamic worlds.

To make this point clear, it is instructive to compute the distance that the bacterium can coast when it stops swimming.

Here is the new homework problem, which asks the student to compute the distance the bacterium can coast.

Section 1.20

Problem 54. When a bacterium stops swimming, it will coast to a stop. Let us calculate how long this coasting takes, and how far it will go.

(a) Write a differential equation governing the speed, v, of the bacterium. Use Newton’s second law with the force given by Stokes law. Be careful about minus signs.

(b) Solve this differential equation to determine the speed as a function of time.

(c) Write the time constant, τ, governing the decay of the speed in terms of the bacterium’s mass, m, its radius, a, and the fluid viscosity, η.

(d) Calculate the mass of the bacterium assuming it has the density of water and it is a sphere with a radius of one micron.

(e) Calculate the time constant of the decay of the speed, for swimming in water having a viscosity of 0.001 Pa s.

(f) Integrate the speed over time to determine how far the bacterium will coast, assuming its initial speed is 20 microns per second.

I won’t solve all the intermediate steps for you; after all, it’s your homework problem. However, below is what Berg has to say about the final result.

A cell moving at an initial velocity of 2 × 10^-3 cm/sec coasts 4 × 10^-10 cm = 0.04 Å, a distance small compared with the diameter of a hydrogen atom! Note that the bacterium is still subject to Brownian movement, so it does not actually stop. The drift goes to zero, not the diffusion.

Berg didn’t calculate the deceleration of the bacterium. If the speed drops from 20 microns per second to zero in one time constant, I calculate the acceleration to be be about 91 m/s², or nearly 10g. This is similar to the maximum allowed acceleration of a plane flying in the Red Bull Air Race. That poor bacterium.

Howard Berg (1934–2021)

Random Walks in Biology,
by Howard Berg.

Look up at the picture of books at the top of this blog, showing my ideal bookshelf. You see Intermediate Physics for Medicine and Biology towering in the center. The small volume two books to the right of IPMB is Random Walks in Biology, by Howard Berg.

Berg died on December 30, 2021. He was the Herchel Smith Professor of Physics in the Rowland Institute at Harvard University. He was known for his studies of flagellar motility and sensory transduction in bacteria, as described in his 2004 book E. coli in Motion.

Berg obtained his bachelor’s degree from Cal Tech, and a PhD from Harvard. He was on the faculty at the University of Colorado, then at Cal Tech, and finally at Harvard. He was a fellow of the American Physical Society and a member of the National Academy of Sciences. In 1984 he and Edward Purcell received the Max Delbrück Prize in Biological Physics from the American Physical Society “for the elucidation of complex biological phenomena, in particular chemotaxis and bacterial locomotion, through simple but penetrating physical theories and brilliant experiments.”

I had the pleasure of meeting Berg at a 2014 Gordon Research Conference about Physics Research and Education: The Complex Intersection of Biology and Physics, held at Mount Holyoke College in South Hadley, Massachusetts. He was a quiet, thoughtful, kind man. I wish I knew him better.

Purcell mentioned Berg in his influential article “Life at Low Reynolds Number” (American Journal of Physics, Volume 45, Pages 3–11, 1977).

I might say what got me into this. To introduce something that will come later, I’m going to talk partly about how microorganisms swim. That will not, however, turn out to be the only important question about them. I got into this through the work of a former colleague of mine at Harvard, Howard Berg. Berg got his Ph.D. with Norman Ramsey, working on a hydrogen maser, and then he went back into biology, which had been his early love, and into cellular physiology. He is now at the University of Colorado at Boulder, and has recently participated in what seems to me one of the most astonishing discoveries about the questions we're going to talk about. So it was partly Howard's work, tracking E. coli and finding out this strange thing about them, that got me thinking about this elementary physics stuff.

Section 4.10 of Intermediate Physics for Medicine and Biology analyzes chemotaxis, and cites Berg’s 1977 paper with Purcell “Physics of Chemoreception” (Biophysical Journal, Volume 20, Pages 119–136). Below is the abstract.

Statistical fluctuations limit the precision with which a microorganism can, in a given time T, determine the concentration of a chemoattractant in the surrounding medium. The best a cell can do is to monitor continually the state of occupation of receptors distributed over its surface. For nearly optimum performance only a small fraction of the surface need be specifically adsorbing. The probability that a molecule that has collided with the cell will find a receptor is Ns/(Ns + πa), if N receptors, each with a binding site of radius s, are evenly distributed over a cell of radius a. There is ample room for many independent systems of specific receptors. The adsorption rate for molecules of moderate size cannot be significantly enhanced by motion of the cell or by stirring of the medium by the cell. The least fractional error attainable in the determination of a concentration c is approximately (TcaD)^−1/2, where D is the diffusion constant of the attractant. The number of specific receptors needed to attain such precision is about a/s. Data on bacteriophage adsorption, bacterial chemotaxis, and chemotaxis in a cellular slime mold are evaluated. The chemotactic sensitivity of Escherichia coli approaches that of the cell of optimum design.

To learn more about Berg's life, education, and career, read his interview with Current Biology.

I will end with Berg’s introduction to his masterpiece Random Walks in Biology. If you want to learn about diffusion, start with Berg’s book.

Biology is wet and dynamic. Molecules, subcellular organelles, and cells, immersed in an aqueous environment, are in continuous riotous motion. Alive or not, everything is subject to thermal fluctuations. What is this microscopic world like? How does one describe the motile behavior of such particles? How much do they move on the average? Questions of this kind can be answered only with an intuition about statistics that very few biologists have. This book is intended to sharpen that intuition. It is meant to illuminate both the dynamics of living systems and the methods used for their study. It is not a rigorous treatment intended for the expert but rather an introduction for students who have little experience with statistical concepts.

The emphasis is on physics, not mathematics, using the kinds of calculations that one can do on the back of an envelope. Whenever practical, results are derived from first principles. No reference is made to the equations of thermodynamics. The focus is on individual particles, not moles of particles. The units are centimeters (cm), grams (g), and seconds (sec).

Topics range from the one-dimensional random walk to the motile behavior of bacteria. There are discussions of Boltzmann’s law, the importance of kT, diffusion to multiple receptors, sedimentation, electrophoresis, and chromatography. One appendix provides an introduction to the theory of probability. Another is a primer on differential equations. A third lists some constants and formulas worth committing to memory. Appendix A should be consulted while reading Chapter 1 and Appendix B while reading Chapter 2. A detailed understanding of differential equations or the methods used for their solution is not required for an appreciation of the main theme of this book.

 

Howard Berg. Marvels of Bacterial Behavior. Part 1.

Howard Berg. Marvels of Bacterial Behavior. Part 2.

The Chain of Reason vs. the Chain of Thumbs

Bully for Brontosaurus,
by Stephen Jay Gould.

I have written previously in this blog about my admiration for evolutionary biologist Stephen Jay Gould and his essays published in his monthly column “This View of Life” in the magazine Natural History. Today, I focus on one of these essays, “The Chain of Reason vs. the Chain of Thumbs,” that is related to a topic in Intermediate Physics for Medicine and Biology. You can find this essay reprinted in Gould’s book Bully for Brontosaurus.

IPMB has a chapter on biomagnetism (the production of magnetic fields by the body) and a section on the possible effects if weak external electric and magnetic fields. Much nonsense has been written about using magnetic fields to treat diseases, including to relieve pain. When did all this silliness begin? Over two hundred years ago.

Gould’s essay describes the fascinating story of the Franz Mesmer, who operated a clinic in Paris in the seventeenth century to treat various illnesses using “animal magnetism.” Gould writes

Franz Anton Mesmer was a German physician who had acquired wealth through marriage to a well endowed widow; connections by assiduous cultivation;… and renown with a bizarre, if fascinating, theory of “animal magnetism” and its role in human health.

Mesmer, insofar as one can find coherence in his ideas at all, claimed that a single (and subtle) fluid pervaded the universe, uniting and connecting all bodies. We give different names to this fluid according to its various manifestations: gravity when we consider planets in their courses; electricity when we contemplate a thunderstorm; magnetism when we navigate by compass. The fluid also flows through organisms and may be called animal magnetism. Disease results from a blockage of this flow, and cure of disease requires a reestablishment of the flux and a restoration of equilibrium.

Cure of illness requires the aid of an “adept,” a person with unusually strong magnetism who can locate the “poles” of magnetic flow on the exterior of a human body and, by massaging these areas, break the blockage within and reestablish the normal flux…

Mesmer's treatments were quite dramatic.

Within a few minutes of mesmerizing, sensitive patients would fall into the characteristic “crisis” taken by Mesmer as proof of his method. Bodies would begin to shake, arms and legs move violently and involuntarily, teeth chatter loudly. Patients would grimace, groan, babble, scream, faint, and fall unconscious.

Gould then tells the story of a Royal Commission established in 1784 by French king Louis XVI to investigate Mesmer’s claims. The commission was headed by American Benjamin Franklin, and included chemist Antoine Lavoisier and medical doctor Joseph Guillotin.

In a clever series of experiments, designed mainly by Lavoisier and carried out at Franklin’s home in Passy, the commissioners made the necessary separations and achieved a result as clear as any in the history of debunking: crises are caused by suggestion; not a shred of evidence exists for any fluid, and animal magnetism, as a physical force, must be firmly rejected.

Gould was impressed by the quality of the commission’s work.

Never in history has such an extraordinary and luminous group been gathered together in the service of rational inquiry by the methods of experimental science. For this reason alone, the Rapport des commissaires chargés par le roi de l’examen du magnétisme animal (Report of the Commissioners Charged by the King to Examine Animal Magnetism) is a key document in the history of human reason. It should be rescued from its current obscurity, translated into all languages, and reprinted by organizations dedicated to the unmasking of quackery and the defense of rational thought.

Nowadays we see a lot of ridiculous claims that magnetic fields can alleviate pain and have other health effects. Julian Whitaker and Brenda Adderly, in their book The Pain Relief Breakthrough, assert that magnets can cure backaches, arthritis, menstrual cramps, carpal tunnel syndrome, sports injuries, and more. Mexican surgeon Isaac Goiz Duran says that his “biomagnetic therapy” can cure diabetes, AIDS, cancer, and Covid-19. All these therapies are based on static magnetic fields, a type of 21st century animal magnetism.

I highly recommend all of Gould’s essays, including this one. Remember the efforts of Franklin, Lavoisier, and Guillotin before you start believing that static magnetic fields can improve your health.