Special Relativity in IPMB

Electricity and Magnetism,
by Edward Purcell.

In Intermediate Physics for Medicine and Biology, Russ Hobbie and I rarely discuss special relativity. We briefly mention that magnetism is a consequence of relativity in Chapter 8 (Biomagnetism) but we don’t develop our study of magnetic fields from this point of view. (If you want to see magnetism analyzed in this way, I suggest looking at the textbook Electricity and Magnetism, by Edward Purcell, which is Volume 2 of the Berkeley Physics Course). We use the relationship between the energy and momentum of a photon, E = pc, in Chapter 15 (Interaction of Photons and Charged Particles with Matter) when analyzing Compton scattering and pair production. And we use Einstein’s famous equation E = mc², relating a particles energy to its rest mass, when calculating the binding energy of nuclei in Chapter 17 (Nuclear Physics and Nuclear Medicine).

The most relativisticish equation we present is in Chapter 15 when analyzing how charged particles (such as protons, electrons, or alpha particles) lose energy when passing through tissue at relativistic speeds. We write

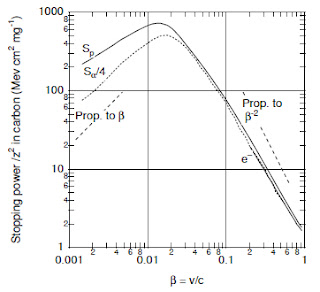
The stopping powers are plotted vs particle speed in the form β = v/c. At low energies (β ≪ 1) β is related to kinetic energy by 

For larger values of β, the relativistically correct expression

was used to convert Fig. 15.17 to 15.18. 

Fig. 15.17

 

Fig. 15.18

Here’s a new homework problem examining the relationship between a particle’s speed and kinetic energy when its speed is near the speed of light.

Section 15.11

Problem 41 ½. A charged particle’s kinetic energy, T, is related to its mass M and its speed, v. We often express speed in terms of the parameter β = v/c, where c is the speed of light.

(a) At low energies (T ≪ Mc², or equivalently β ≪ 1), show that Eq. 15.47 is consistent with the familiar expression from classical mechanics, T = ½ mv².

(b) Show that Equation 15.48 (the relativistically correct relationship between β and T) reduces to Eq. 15.47 when T ≪ Mc².

(c) Plot β versus T/Mc², both in a linear plot (0 < T/Mc² < 3) and in a log-log plot (0.0001 < T/Mc² < 100).

(d) Take a few data points from Fig. 15.17 for a proton, replot them in Fig. 15.18, where the dependent variable is β, not T. See how well they match. Be sure to adjust for the different units for Stopping Power in the two plots.