Taylor's Series

In Appendix D of the 5th edition of Intermediate Physics for Medicine and Biology, Russ Hobbie and I review Taylor’s Series. Our Figures D.3 and D.4 show better and better approximations to the exponential function, e^x, found by using more and more terms of its Taylor’s series. As we add terms, the approximation improves for small |x| and diverges more slowly for large |x|. Taking additional terms from the Taylor’s series approximates the exponential by higher and higher order polynomials. This is all interesting and useful, but the exponential looks similar to a polynomial, at least for positive x, so it is not too surprising that polynomials do a decent job approximating the exponential.

A more challenging function to fit with a Taylor’s Series would look nothing like a polynomial, which always grows to plus or minus infinity at large |x|. I wonder how the Taylor’s Series does approximating a bounded function; perhaps a function that oscillates back and forth a lot? The natural choice is the sine function.

The Taylor’s Series of sin(x) is

sin(x) = x – x³/6 + x⁵/120 – x⁷/5040 + x⁹/362880 - …

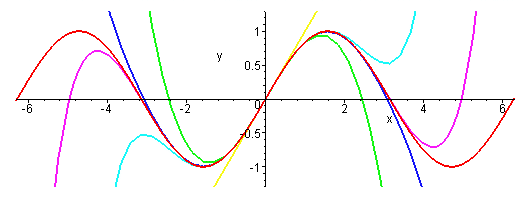
The figure below shows the sine function and its various polynomial approximations.

The sine function and its various polynomial approximations,
from: http://www.peterstone.name/Maplepgs/images/Maclaurin_sine.gif

The red curve is the sine function itself. The simplest approximation is simply sin(x) = x, which gives the yellow straight line. It looks good for |x| less than one, but quickly diverges from sine at large |x|. The green curve is sin(x) = x – x³/6. It rises to a maximum and then falls, much like sin(x), but  heads off to plus or minus infinity relatively quickly. The cyan curve is sin(x) = x – x³/6 + x⁵/120. It captures the first peak of the oscillation well, but then fails. The royal blue curve is sin(x) = x – x³/6 + x⁵/120 – x⁷/5040. It is an excellent approximation of sin(x) out to x = π. The violet curve is sin(x) = x – x³/6 + x⁵/120 – x⁷/5040 + x⁹/362880. It begins to capture the second oscillation, but then diverges. You can see the Taylor’s Series is working hard to represent the sine function, but it is not easy.

Appendix D in IPMB gives a table of values of the exponential and its different Taylor’s Series approximations. Below I create a similar table for the sine. Because the sine and all its series approximations are odd functions, I only consider positive values of x.

A table of values for sin(x) and its various polynomial approximations.

One final thought. Russ and I title Appendix D as “Taylor’s Series” with an apostrophe s. Should we write “Taylor Series” instead, without the apostrophe s? Wikipedia just calls it the “Taylor Series.” I’ve seen it both ways, and I don’t know which is correct. Any opinions?