|
| “Prelude No. 1,” from the Well-Tempered Clavichord, by Johann Sebastian Bach. I played it (or tried to play it) back when I was 15 years old. |
Most of my blog posts are about physics applied to medicine and biology, but today I want to talk about music. This topic may not seem relevant to Intermediate Physics for Medicine and Biology, but I would argue that it is. Music is, after all, as much about the human perception of sound as about sound itself. So, let’s talk about how we sort the different frequencies into notes.
Below I show a musical keyboard, like you would find on a piano.
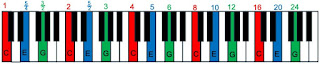
Each key corresponds to a different pitch, or note. I want to discuss the relationships between the different notes. We have to start somewhere, so let’s take the lowest note on the keyboard and call it C. It will have some frequency, which we’ll call our base frequency. On the piano, this frequency is about 33 Hz, but for our purposes that doesn’t matter. We will consider all frequencies as being multiples of this base frequency, and take our C as having a frequency of 1.
When you double the frequency, our ear perceives that change as going up an octave. So, one octave above the first C is another C, with frequency 2.
Of course, that means there’s another C with frequency 4, and another with frequency 8, and so on. We get a whole series of C’s.
Now, if you pluck a string held down at both ends, it can produce many frequencies. In general, it produces frequencies that are multiples of a fundamental frequency f, so you get frequency f plus “overtone” frequencies 2f, 3f, 4f, 5f, etc. As we noted earlier, we don’t care about the frequency itself but only how different frequencies are related. If the fundamental frequency is a C with frequency 1, the first overtone is one octave up (with a frequency 2), another C. The second overtone has a frequency 3. That corresponds to a different note on our keyboard, which we’ll call G.
You could raise or lower G by octaves and still have the same note (like we did with C), so you have a whole series of G’s, including 3/2 which is between C’s corresponding to frequencies 1 and 2. When two notes have frequencies such that the upper frequency is 3/2 times the lower frequency (a 3:2 ratio), musicians call that a “fifth,” so G is a fifth above C.
Let’s keep going. The next overtone is 4, which is two octaves above the fundamental, so it’s one of the C’s. But the following overtone, 5, gives us a new note, E.
As always, you can go up or down by octaves, so we get a whole series of E’s.
C and E are related by a ratio of 5:4 (that is, E has a frequency 5/4 times the C below it), which musicians call a “third.” The notes C, E, and G make up the “C major chord.”
The next overtone would be 6, but we already know 6 is a G. The overtone 7 doesn’t work. Apparently a frequency ratio of 7 is not one that we find pleasant (at least, not to those of us who have been trained on western music), so we’ll skip it. Overtone 8 is another C, but we get a new note with overtone 9 (and all its octaves up and down, which I’ll stop repeating again and again). We’ll call this note D, because it seems to fit nicely between C and E.
The D right next to our base note C has a frequency of 9/8.
Next is overtone 10 (an E), then 11 (like 7, it doesn’t work), 12 (a G), 13 (nope), 14 (no because it’s an octave up from 7), and finally 15, a new note we’ll call B.
We could go on, but we don’t perceive many of the higher overtones as harmonious, so let’s change track. There’s nothing special about our base note, the C on the far left of our keyboard. Suppose we wanted to use a different base note. What note would we use if we wanted it to be a fifth below C? If we started with a frequency of 2/3, then a fifth above that frequency would be 2/3 times 3/2 or 1, giving us C. We’ll call that new base frequency F. It’s off our keyboard to the left, but its octaves appear, including 4/3, 8/3, etc.
What if we want to build a major chord based on F. We already have C as a fifth above F. What note is a third above F? In other words, start at 2/3 and multiply by 5/4 (a third), to get 10/12 which simplifies to 5/6. That’s off the keyboard too, but its octaves 5/3, 10/3, 20/3, etc. appear. Let’s call it A. So a major chord in the key of F is F, A, and C.
Does this work for other base frequencies? Try G (3/2). Go up a fifth from G and you get 9/4, which is a D. Go up a third from G and you get 15/8, which is a B. So G, B, and D make up a major chord in the key of G. It works again!
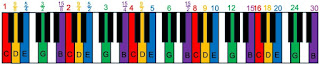
So now it looks like we’re done. We’ve given names and frequencies to all the notes: C (1), D (9/8), E (5/4), F (4/3), G (3/2), A (5/3), and B (15/8). This collection of frequencies is called “just intonation,” with “just” used in the sense of fair and honest. If you play a song in the key of C, you use only those notes and frequencies and it sounds just right.
What about those strange block notes between some, but not all, of the white notes? How do we determine their frequencies? For example, start at D (9/8) for your base note and build a major chord. First you and go up a third and get 9/8 times 5/4, or 45/32. That note, corresponding to the black key just to the right of F, is F-sharp (or F♯). To express the frequency as a decimal, 45/32 = 1.406, which is midway between F (4/3 = 1.333) and G (3/2 = 1.500). We could continue working out all the frequencies for the various sharps and flats, but we won’t. It gets tedious, and there is an even more interesting and surprising feature to study.
To complete our D major chord, we need to to determine what note is a fifth above D. You get D (9/8) times a fifth (3/2), or 27/16 = 1.688. That is almost the same as A (5/3 = 1.667), but not quite. It’s too close to A to correspond to A-sharp. It’s simply an out-of-tune A. In other words, using the frequencies we have worked out above, if you start with C as your base (that is, you play in the key of C) your G (a fifth) corresponds to a frequency ratio of 5/3 = 1.667. If you play, however, using D as your base (you play in the key of D), your A (what should be a fifth above D) has a frequency ratio of 27/16 = 1.688. Different keys have different intonations. Yikes! This is not a problem with only the key of D. It happens again and again for other keys. The intonation is all messed up. You either play in the key of C, or you play out of tune.
To avoid this problem, nowadays instruments are tuned so that there are 12 steps between octaves (the steps includes both the white and black keys), where each step corresponds to a frequency ratio of 21/12 = 1.0595. A fifth (seven steps) is then 27/12 = 1.498, which is not exactly 3/2 = 1.500 but is pretty close and—importantly—is the same for all keys. A third is 24/12 = 1.260, which is not 5/4 = 1.250 but is not too bad. A keyboard with frequencies adjusted in this way is called “well-tempered.” It means that all the keys sound the same, although each is slightly out of tune compared to just intonation. You don’t have to have your piano tuned every time you change keys.
Johann Sebastian Bach wrote a lovely set of piano pieces called The Well-Tempered Clavichord that showed off the power of well-tempered tuning. My copy of the most famous of these pieces is shown in the photo at the top of this post. Listen to it and other glorious music by Bach below.
https://www.youtube.com/watch?v=iWoI8vmE8bI
Bach’s “Cello Suite No. 1,” played by Yo Yo Ma.
https://www.youtube.com/watch?v=Rx_IibJH4rA
Bach’s “Toccata and Fugue in D minor.”
https://www.youtube.com/watch?v=erXG9vnN-GI
Bach’s “Jesu, Joy of Man’s Desiring,” performed by Daniil Trifonov.
https://www.youtube.com/watch?v=wEJruV9SPao
Bach’s “Air on the G String.”
https://www.youtube.com/watch?v=pzlw6fUux4o
Bach and Gounod’s “Ave Maria,” sung by Andrea Bocelli.