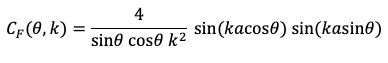|
“An Assessment of Illness in
U.S. Government Employees and
their Families at Overseas Embassies”
(2020) The National Academies Press.
|
Recently, a
National Academies report examined the illness of staff at overseas embassies.
National Academies of Sciences, Engineering, and Medicine. 2020. “An Assessment of Illness in U.S. Government Employees and their Families at Overseas Embassies.” Washington, DC: The National Academies Press.
The summary of the report begins
In late 2016, U.S. Embassy personnel in Havana, Cuba, began to report the development of an unusual set of symptoms and clinical signs. For some of these patients, their case began with the sudden onset of a loud noise, perceived to have directional features, and accompanied by pain in one or both ears or across a broad region of the head, and in some cases, a sensation of head pressure or vibration, dizziness, followed in some cases by tinnitus, visual problems, vertigo, and cognitive difficulties. Other personnel attached to the U.S. Consulate in Guangzhou, China, reported similar symptoms and signs to varying degrees, beginning in the following year. As of June 2020, many of these personnel continue to suffer from these and/or other health problems. Multiple hypotheses and mechanisms have been proposed to explain these clinical cases, but evidence has been lacking, no hypothesis has been proven, and the circumstances remain unclear.
The Department of State (DOS), as part of its effort to inform government
employees more effectively about health risks at posts abroad, ascertain potential causes of the
illnesses, and determine best medical practices for screening, prevention, and treatment for both
short and long-term health problems, asked the National Academies of Sciences, Engineering,
and Medicine (the National Academies) to provide independent, expert guidance.
Then, under the heading of “Plausible Mechanisms,” the summary states
The committee found the unusual presentation of acute, directional or location-specific
early phase signs, symptoms and observations reported by DOS employees to be consistent with
the effects of directed, pulsed radio frequency (RF) energy.
I’m reluctant to disagree with a report from the National Academies. I wasn’t a member of the committee, I wasn’t consulted by them, and I haven’t analyzed the data myself. Moreover, I’m disturbed by the recent tendency of political leaders to ignore science (for example, on the
Covid-19 pandemic and
climate change), so I hesitate to reject a review by some of the nation’s top scientists and medical doctors. Nevertheless, I don’t find this report convincing.
As I’ve written before in this blog, I’m skeptical that
radio-frequency or
microwave radiation can explain these effects.
The report states that
Low-level RF exposures typically deposit energy below the threshold for significant
heating (often called “nonthermal” effects), while high-level RF exposures can provide enough
energy for significant heating (“thermal” effects) or even burns, and for stimulation of nervous
and muscle tissues (“shock” effects)... While much of the general public discussion
on RF biological effects has focused on cancer, there is a growing amount of data demonstrating
a variety of non-cancer effects as well, in addition to those associated with thermal heating.
The absence of certain observed phenomena can also help to constrain potential RF
source characteristics. For example, the absence of reporting of a heating sensation or internal
thermal damage may exclude certain types of high-level RF energy.
Microwaves affect the body if they’re strong enough to heat tissue (like in a microwave oven). But low-level radio-frequency and microwave effects are less well established (to put it politely). I don’t think there is a growing amount of reliable data demonstrating effects from RF electromagnetic radiation. The same issue arises when discussing the safety of cellular phone radiation (I fear this report will be used by some to support
dubious claims of
5G hazards).
The report twice cites studies by
Martin Pall.
As I said previously in this blog “Pall’s central hypothesis is that cell phone radiation affects calcium ion channels, which if true could trigger a cascade of biological effects…. I don’t agree with Pall’s claims.” Neither do
Ken Foster and
John Moulder (both cited frequently in
Intermediate Physics for Medicine and Biology), who
wrote that
Despite some level of public controversy and an ongoing stream of reports of highly variable quality of biological effects of RF energy... health agencies consistently conclude that there are no proven hazards from exposure to RF fields within current exposure limits.
The National Academies report emphasizes the
Frey effect, in which pulsed electromagnetic radiation causes slight local heating, resulting in tiny transient changes in pressure that can be sensed by the
inner ear. In a previous post,
I wrote
I am no expert on thermoelastic effects, but it seems plausible that they could be responsible for the perception of sound by embassy workers in Cuba. By modifying the shape and frequency of the microwave pulses, you might even induce sounds more distinct than vague clicks. However, I don’t know how you get from little noises to brain damage and cognitive dysfunction. My brain isn’t damaged by listening to clicky sounds.
The most ridiculous paragraph in the report relates
transcranial magnetic stimulation—a technique I worked on while at the
National Institutes of Health—to the Frey effect.
If a Frey-like effect can be induced on central nervous system tissue responsible for space
and motion information processing, it likely would induce similarly idiosyncratic responses.
More general neuropsychiatric effects from electromagnetic stimuli are well-known and are
being used increasingly to treat psychiatric and neurologic disorders. In 2008, the Food and DrugAdministration (FDA) approved transcranial magnetic stimulation (TMS) to treat major
depression in adults who do not respond to antidepressant medications... Ten years
later, the FDA approved office-based TMS as a treatment for obsessive compulsive disorder
(OCD)... and portable TMS to treat migraine.
Magnetic stimulation uses large (about 1 Tesla) magnetic fields, and works at low frequencies (1–10 kHz, which are the frequencies that nerves operate at, and are well below the microwave range). Much higher frequencies are unlikely to activate nerves, and such strong magnetic fields will have tell-tale signs. For instance, one way to demonstrate the power of TMS is to place a quarter at the center of a coil and deliver a single pulse. The quarter shoots up into the air, sometimes denting a ceiling tile (I admit, this wasn’t the safest parlor trick I’ve ever witnessed). TMS only activates the brain when the coil is held within a few centimeters of the head. Trying to generate magnetic stimulation remotely would require Herculean magnetic fields that would certainly be noticed (anything metallic would start flying around and heating up). The reason the Frey effect works with weak fields is the extreme sensitivity of the human ear for detecting minuscule pressure oscillations. If the authors of the report think citing transcranial magnetic stimulation is appropriate as evidence to support the plausibility of a Frey-like effect, then they don’t understand the basic physics of how electric and magnetic fields interact with the body.
My view is much closer to that expressed in the article “Havana Syndrome Skepticism” by Robert Bartholomew, which was published in eSkeptic, the email newsletter of the Skeptics Society.
The Frey effect is named after Allan Frey, a pioneer in radiation research. But there are many problems with the explanation. It is highly speculative, and none of the panel members appeared to be experts on the biological impact of microwaves and the Frey effect. Someone who is a specialist on the effect, University of Pennsylvania bioengineer Kenneth Foster, is critical of the report, observing that there is no evidence that the Frey effect can cause injuries. Furthermore, the effect requires a tremendous amount of energy to create a sound that is barely audible... Foster should know, in 1974, he and Edward Finch were the first scientists to describe the mechanism involved in the effect while working at the Naval Medical Research Institute in Maryland...
Foster views any link between his eponymous effect and Havana Syndrome as pure fantasy. “It is just a totally incredible explanation for what happened to these diplomats…. It’s just not possible. The idea that someone could beam huge amounts of microwave energy at people and not have it be obvious defies credibility...” The former head of the Electromagnetics division of the Environmental Protection Agency, Ric Tell, also views the microwave link as science fiction. Tell spent decades working on standards for safe exposure to electromagnetic radiation, including microwaves. “If a guy is standing in front of a high-powered radio antenna — and it’s got to be high, really high — then he could experience his body getting warmer,” Tell said. “But to cause brain-tissue damage, you would have to impart enough energy to heat it up to the point where it’s cooking. I don’t know how you could do that, especially if you were trying to transmit through a wall. It’s just not plausible,” he said.
At the risk of sounding like a grumpy old curmudgeon, I don’t believe the National Academies report. I don’t agree that directed radio-frequency or microwave energy is the most likely explanation for the “Havana Syndrome.” I don’t have a better explanation, but I don’t accept theirs. It’s not consistent with what we know about how electromagnetic fields interact with biological tissue.