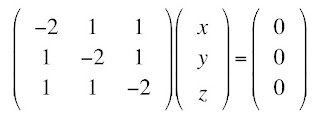An Analytical Example of Filtered Back Projection

One of my hobbies is to find tomography problems that can be solved analytically. I know this is artificial—all tomography for medical imaging uses numerical computation—but as a learning tool analytical analysis helps build insight. I have some nice analytical examples using the Fourier method to solve the tomography problem (see homework problems 26 and 27 in chapter 12 of Intermediate Physics for Medicine and Biology), but I don't have a complete analytical example to illustrate the filtered back projection method (see a previous post for a partial example). Russ Hobbie and I do include a numerical example in section 12.6 of IPMB. I have always wondered if I can do that example analytically. Guess what. I can! Well, almost.

Start with a top-hat function for your object

If we set x = 0, we can plot it as function of y.

The projection of this function is given in IPMB; Homework Problem 36 asks the reader to derive it.

Because the object looks the same from all directions, the projection is independent of the angle. Below is a plot of the projection as a function of x'. It is identical to the top panel of IPMB's Figure 12.22.

The next step is to filter the projection, which means we have to take its Fourier transform, multiply the transform by a high-pass filter, and then do the inverse Fourier transform. The Fourier transform of the projection is

This integral is not trivial, but Abramowitz and Stegun’s Handbook of Mathematical Functions With Formulas, Graphs and Mathematical Tables contains (Page 360, Equation 9.1.20)

where J₁ is a first-order Bessel function (see Homework Problem 10). Because the projection is an even function, the sine part of the Fourier transform vanishes.

Filtering is easy; multiply by |k|/2π. The result is

To find the inverse Fourier transform, we need

This integral appears in Abramowitz and Stegun (Page 487, Equation 11.4.37)

After some simplification (which I leave to you), the filtered projection becomes

Below is a plot of the filtered projection, which you should compare with the middle panel of Fig. 12.22. It looks the same as the plot in IPMB, except in the numerical calculation there is some ringing near the discontinuity that is not present in the analytical solution

The final step is back projection. Because the projection is independent of the angle, we can calculate the back projection along any radial line, such as along the y axis

If |y| is less than a, the back projection is easy: you just get 1. Thus, the filtered back projection is the same as the object, as it should be. If |y| is greater than a, the result should be zero. This is where I get stuck; I cannot do the integral. If any reader can solve this integral (and presumably show that it gives zero), I would greatly appreciate hearing about it. Below is a plot of the result; the part in red is what I have not proven yet. Compare this plot with the bottom panel of Fig. 12.22.

What happens if you do the back projection without filtering? You end up with a blurry image of the object. I can solve this case analytically too. For |y| less than a, the back projection without filtering is

which is 4a times the complete elliptic integral of the second kind

For |y| greater than a, you get the more complicated expression

which is the incomplete elliptic integral of the second kind

The trickiest part of the calculation is determining the upper limit on the integral, which arises because for some angles the projection is zero (you run into the same situation in homework problem 35, which I highly recommend). Readers who are on the ball may worry that the elliptic integral is tabulated only for kappa less than one, but there are ways around this (see Abramowitz and Stegun, Page 593, Equation 17.4.16). When I plot the result, I get

which looks like Fig. 12.23 in IPMB.

So, now you have an analytical example that illustrates the entire process of filtered back projection. It even shows what happens if you forget to filter before back projecting. For people like me, the Bessel functions and elliptic integrals in this calculation are a source of joy and beauty. I know that for others they may be less appealing. To each his own.

I’ll rely on you readers to fill in the one missing step: show that the filtered back projection is zero outside the top hat.

Five Generations

A five generation picture.

When my first daughter Stephanie was born, we included her in this photo of five generations. From left to right are my maternal grandmother, my great-grandmother (born 1889), my daughter Stephanie (born 1988), me, and my mom. My great grandmother lived to be over 100 years old. I remember playing poker with her when I was young; she generally won and kept the money!

All five editions of
Intermediate Physics for Medicine and Biology.

Recently I took another five-generation photo. There now exist five generations (editions) of Intermediate Physics for Medicine and Biology. My office is one of the few places you can find all five on one bookshelf. I was coauthor on the fourth and fifth editions; the first three editions were authored by Russ Hobbie alone.

Suki with all five editions of
Intermediate Physics for Medicine and Biology.

The yellow book is the first edition of IPMB, published by John Wiley and Sons in 1978. The blue version with the yellow sine wave on the cover is the second edition, again published by Wiley in 1988. The green cover is the third edition, published by Springer with AIP Press in 1997. The blue fourth edition was published by Springer alone in 2007. Finally, the blue/purple fifth edition, again published by Springer, appeared in 2015. My dog Suki seems to like them all.

All five editions of
Intermediate Physics for Medicine and Biology.

I have a special fondness for the first edition, which I bought for a class taught by my PhD advisor John Wikswo at Vanderbilt University in the early 1980s (price: $31.95). That is where I learned much of my biological and medical physics. When Russ was preparing the second edition, he asked John and I to create some three-dimensional figures of the electrical potential and magnetic field of a nerve axon. There figures have appeared in each subsequent edition of IPMB, and are Figs. 7.13 and 8.14 in the fifth. My third edition is pretty beat up. It is the textbook I taught out of for several years after I arrived at Oakland University. The fourth and fifth editions I know best, as I helped write them (although Russ remains the primary force behind every edition).

All five editions of
Intermediate Physics for Medicine and Biology.

IPMB has changed over the years. The first seven chapters are the same in all versions, but Russ added chapters on charged membranes and biomagnetism in the second edition. The first edition’s chapter on signal analysis split into two in the second: one on one-dimensional signal analysis and another on two-dimensional images. The 4th edition picked up a chapter on ultrasound. The first edition’s chapter on x-rays fissioned into a chapter on how x-rays interact with tissue and a chapter on the medical uses of x-rays. Finally, the second edition introduced a chapter on magnetic resonance imaging. Early editions featured a figure on the cover. I particularly like the first edition’s electrocardiogram picture (Fig. 7.16 in the 5th edition). Russ and I planned on using a computed tomography illustration, Fig. 12.12, on the 4th edition cover, but Springer opted to use a generic cover with no figure.

Me holding all five editions of
Intermediate Physics for Medicine and Biology.

Working on revisions of IPMB has been a pleasure and an honor. But really, the five generations of IPMB is a tribute to Russ Hobbie and his vision of advancing the teaching of physics in medicine and biology, which he has pursued over nearly four decades. I hope you find the book as useful as I have.

Trivial Pursuit IPMB

Trivial Pursuit.

Trivial Pursuit is a popular and fun board game invented in the 1980s. While playing it, you learn many obscure facts (trivial, really).

When my daughter Kathy was in high school, she would sometimes test out of a subject by studying over the summer and then taking an exam. Occasionally I would help her study by skimming through her textbook and creating Trivial Pursuit-like questions. We would then play Trivial Pursuit using my questions instead of those from the game. I don’t know if it helped her learn, but she always passed those exams.

Readers of Intermediate Physics for Medicine and Biology may want a similar study aid to help them learn about biological and medical physics. Now they have it! At the book website you can download 100 game cards for Trivial Pursuit: IPMB. To play, you will need the game board, game pieces, and instructions of the original Trivial Pursuit, but you replace the game cards by the ones I wrote.

The game pieces for Trivial Pursuit.

In case you have never played, here are the rules in a nutshell. The board has a circle with spots of six colors. You roll a die and move your game piece around the circle, landing on the spots. Your opponent asks you a question about a topic determined by the color. If you answer correctly you roll again; if you are wrong your opponent rolls. There are special larger spots where a correct answer gets you get a little colored wedge. The first person to get all six colored wedges wins.

The original version of Trivial Pursuit had topics such as sports or literature. The Trivial Pursuit: IPMB topics are

• Numbers and Units (blue)
• People (pink)
• Anatomy and Physiology (yellow)
• Biological Physics (brown)
• Medical Physics (green)
• Mathematics (orange).

One challenge of an interdisciplinary subject like medical and biological physics is that you need a broad range of knowledge. I suspect mathematicians will find the math questions to be simple, but the biologists may find them difficult. Physicists may be unfamiliar with anatomy and physiology, and chemists may find all the topics hard. The beauty of the game is that it rewards a broad knowledge across disciplines.

A game card for Trivial Pursuit.

Many may find the People section most challenging. I suggest you only require the player to know the person’s last name, although the first name is also given on my game card. In Units and Numbers I generally only require numbers to be known approximately. The goal is to have an order-of-magnitude knowledge of biological parameters and physical constants. Many questions ask you to estimate the size of an object, like in Section 1.1 of IPMB. For the math and physics questions you may need a pencil and paper handy, because some of the questions contain equations. You can’t simply show your opponent the equation on the game card, because both the questions and answers are together. This is unlike the real Trivial Pursuit game cards, which had the answers on the back. Unfortunately, such two-sided cards are difficult to make.

I know the game is not perfect. Some questions are truly trivial and others ask for some esoteric fact that no one would be expected to remember. Some questions may have multiple answers of which only one is on the card. You can either print out the game cards (requiring 100 pieces of paper) or use a laptop or mobile device to view the pdf. I try to avoid repetitions, but with 100 game cards some may have slipped in inadvertently.

Trivial Pursuit.

I may try using Trivial Pursuit: IPMB next time I teach Biological Physics (PHY 325) or Medical Physics (PHY 326) here at Oakland University. It would be excellent for, say, the last day of class, or perhaps a day when I know many students will be absent (such as the Wednesday before Thanksgiving). It doesn’t teach important high-level skills, such as learning to use mathematical models to describe biology, or understanding how physics constrains the way organisms evolve. You can’t teach a complex and beautiful subject like tomography using Trivial Pursuit. But for learning a bunch of facts, the game is useful.

Enjoy!

Science Blogging

Science Blogging:
The Essential Guide,
by Wilcox, Brookshire, and Goldman.

After writing this blog for nine years, I decided it is time to figure out what I’m doing. So I read the book Science Blogging: The Essential Guide (Yale University Press, 2016), edited by Christie Wilcox, Bethany Brookshire, and Jason Goldman. Their preface concludes

By bringing together some of the most experienced voices from around the science blogosphere, we hope this book will have something to teach everyone. Whether you’re just getting started, have some blog posts under your belt, or are looking for fresh inspiration, you are not alone. The science communication community may seem overwhelming, but it’s friendly. Dive in and show us what you can do. Seriously. Tweet us and show us your stuff. And use our hashtag, #SciBlogGuide, and find us online at http://www.theopennotebook.com/science-blogging-essential-guide.

I enjoyed Science Blogging, but oddly I didn’t feel connected to what many of the authors discussed. What you are reading now is less a science blog and more an auxiliary resource for the textbook that Russ Hobbie and I wrote: Intermediate Physics for Medicine and Biology. My goal is to provide materials that help instructors use the book in their classes, and extend and update topics that readers of the book are interested in. I view this blog as being similar to the solutions manual and the errata: it augments the book. The closest Science Blogging came to my blog is in the last chapter, “From Science Blog to Book,” by Brian Switek. But his chapter was primarily about using a blog as a springboard to writing a book, and only at the end of his chapter did he add that “there’s no reason to stop blogging when your book comes out.” I did the opposite. My blog began after Russ and I published the 4th edition of IPMB, and my goal was to improve sales. Has it worked? It’s hard to say, because our sales have never been spectacular. I hope it has had some impact.

Matt Shipman’s chapter on “Metrics” inspired me to look into the statistics for my blog. The post with by far the most page views is Frank Netter, Medical Illustrator. While I liked that post, I don’t know why it has more than three times as many page views as the next most viewed entry. In fact, I see no correlation between the number of page views and what I consider quality or relevance.

Bethany Brookshire wrote a chapter on “Science Blogging and Money.” I like money as much as the next guy, but I don’t subject my dear readers to ads. Hobbieroth.blogspot.com is add-free. There is one exception: each blog post contains a reference to IPMB. I guess that is a sort of advertisement.

Several authors talked about building a following using Twitter. I don’t tweet, but should I? Do you want to hear about IPMB several times a day? I don’t think so. I’ll continue posting once a week; every Friday morning, like clockwork. By the way, what’s a hashtag? I always thought I was a hep cat, but I guess not.

My favorite chapter was Ed Yong’s essay about “Building an Audience for Your Blog.” Accumulating a large following is not my goal; I am more a citation man than a page view man. Yong’s advice is that “you have to have something worth writing about, and you have to write it well.” That sums it up nicely. I think that physics applied to medicine and biology is something worth writing about; I hope I write it well. Yong also writes “picture your ideal readers in your head: who are they?” While I hope anyone interested in biological physics or medical physics will find my blog useful, I don’t write it for such a broad audience. I write it for the students and teachers using Intermediate Physics for Medicine and Biology. And, I write it for myself. I hope you enjoy it. I do.

The Four Equations of Old Quantum Theory

Subtle is the Lord,
by Abraham Pais.

In ‘Subtle is the Lord…”: The Science and the Life of Albert Einstein, Abraham Pais illustrates the old quantum theory using four equations:

• Planck’s law for blackbody radiation, the oldest equation in quantum theory,
• Einstein’s 1905 equation for the energy of photoelectrons ejected from a metallic surface irradiated by light, the oldest equation in the quantum theory describing how radiation and matter interact,
• The equation for the Rydberg constant derived by Niels Bohr in 1913, the oldest equation in the quantum theory of atomic structure, and
• Einstein’s 1906 equation for the specific heat of a solid, the oldest equation in the quantum theory of solid state physics.

Does Intermediate Physics for Medicine and Biology introduce students to these four landmark equations? Let us look one by one.

Planck’s law

Planck’s law for blackbody radiation is presented in Sec. 14.8 of IPMB as our Eq. 14.38 (see last week’s post in this blog). Although we don’t delve into the history of this equation, we do analyze it in detail, deriving the Stefan-Boltzmann law and the Wien displacement law (the peak frequency of radiation increases with temperature). Pais writes “It is remarkable that the old quantum theory would originate from the analysis of a problem as complex as blackbody radiation. From 1859 to 1926, this problem remained at the frontier of theoretical physics, first in thermodynamics, then in electromagnetism, then in the old quantum theory, and finally in quantum statistics.”

The Photoelectric Effect

IPMB presents the photoelectric effect equation as Eq. 15.3 in the chapter about the Interaction of Photons and Charged Particles with Matter. However, it is not discussed in the context of light shining on a metal surface. Rather, it describes a photon interacting with tissue. “In the photoelectric effect…the photon is absorbed by the atom and a single electron, called a photoelectron, is ejected. The initial photon energy is equal to…the kinetic energy of the electron…plus the excitation energy of the atom.” The photoelectric effect is the primary mechanism by which low energy photons (soft x-rays, up to photon energies of roughly 100 keV) interact with tissue. It is the main contributor to the tissue cross section at low energies.

The Rydberg Constant

The atomic energy levels of hydrogen, as derived by Niels Bohr, are presented in Eq. 14.8 of IPMB. However, the Rydberg constant is not mentioned in our book except in homework problem 14.4, where the student is asked to “Find an expression for [the Rydberg constant] in terms of fundamental constants.”

The Specific Heat of a Solid

Sorry, but you won’t find Einstein’s equation for the specific heat of a solid in IPMB. In Section 3.1 we do discuss heat capacity. But biology occurs at fairly high temperatures, and human biology is essentially isothermal. The power of Einstein’s equation becomes evident when you examine how the specific heat decreases as the temperature approaches absolute zero. This behavior is critical for understanding low temperature physics, but is irrelevant for physics applied to medicine and biology.

Chernobyl

The Chernobyl nuclear reactor.

The worst nuclear accident ever happened thirty years ago this week: Chernobyl. Below are excerpts from a UNSCEAR (United Nations Scientific Committee on the Effects of Atomic Radiation) website about the disaster.

Summary

The accident at the Chernobyl nuclear reactor that occurred on 26 April 1986 was the most serious accident ever to occur in the nuclear power industry. The reactor was destroyed in the accident and considerable amounts of radioactive material were released to the environment. The accident caused the deaths, within a few weeks, of 30 workers and radiation injuries to over a hundred others. In response, the authorities evacuated, in 1986, about 115,000 people from areas surrounding the reactor and subsequently relocated, after 1986, about 220,000 people from Belarus, the Russian Federation and Ukraine .…

Among the residents of Belarus, the Russian Federation and Ukraine, there had been up to the year 2005 more than 6,000 cases of thyroid cancer reported in children and adolescents who were exposed at the time of the accident, and more cases can be expected during the next decades. Notwithstanding the influence of enhanced screening regimes, many of those cancers were most likely caused by radiation exposures shortly after the accident. Apart from this increase, there is no evidence of a major public health impact attributable to radiation exposure two decades after the accident. There is no scientific evidence of increases in overall cancer incidence or mortality rates or in rates of non-malignant disorders that could be related to radiation exposure. The incidence of leukaemia in the general population, one of the main concerns owing to the shorter time expected between exposure and its occurrence compared with solid cancers, does not appear to be elevated. Although those most highly exposed individuals are at an increased risk of radiation-associated effects, the great majority of the population is not likely to experience serious health consequences as a result of radiation from the Chernobyl accident. Many other health problems have been noted in the populations that are not related to radiation exposure.

Release of Radionuclides

The accident at the Chernobyl reactor happened during an experimental test of the electrical control system as the reactor was being shut down for routine maintenance. The operators, in violation of safety regulations, had switched off important control systems and allowed the reactor, which had design flaws, to reach unstable, low-power conditions. A sudden power surge caused a steam explosion that ruptured the reactor vessel, allowing further violent fuel-steam interactions that destroyed the reactor core and severely damaged the reactor building. Subsequently, an intense graphite fire burned for 10 days. Under those conditions, large releases of radioactive materials took place.

The radioactive gases and particles released in the accident were initially carried by the wind in westerly and northerly directions. On subsequent days, the winds came from all directions. The deposition of radionuclides was governed primarily by precipitation occurring during the passage of the radioactive cloud, leading to a complex and variable exposure pattern throughout the affected region, and to a lesser extent, the rest of Europe.

Exposure of Individuals

The radionuclides released from the reactor that caused exposure of individuals were mainly iodine-131, caesium-134 and caesium-137. Iodine-131 has a short radioactive half-life (eight days), but it can be transferred to humans relatively rapidly from the air and through consumption of contaminated milk and leafy vegetables. Iodine becomes localized in the thyroid gland.….

The isotopes of caesium have relatively longer half-lives (caesium-134 has a half-life of 2 years while that of caesium-137 is 30 years). These radionuclides cause longer-term exposures through the ingestion pathway and through external exposure from their deposition on the ground. Many other radionuclides were associated with the accident, which were also considered in the exposure assessments.

Average effective doses to those persons most affected by the accident were assessed to be about 120 mSv for 530,000 recovery operation workers, 30 mSv for 115,000 evacuated persons and 9 mSv during the first two decades after the accident to those who continued to reside in contaminated areas.… Maximum individual values of the dose may be an order of magnitude and even more …. [As discussed in Chapter 16 of Intermediate Physics for Medicine and Biology, the average annual background dose is about 3 mSv.]

Conclusions

The accident at the Chernobyl nuclear power plant in 1986 was a tragic event for its victims, and those most affected suffered major hardship. Some of the people who dealt with the emergency lost their lives. Although those exposed as children and the emergency and recovery workers are at increased risk of radiation-induced effects, the vast majority of the population need not live in fear of serious health consequences due to the radiation from the Chernobyl accident. For the most part, they were exposed to radiation levels comparable to or a few times higher than annual levels of natural background, and future exposures continue to slowly diminish as the radionuclides decay. Lives have been seriously disrupted by the Chernobyl accident, but from the radiological point of view, generally positive prospects for the future health of most individuals should prevail.

More about the physics of the disaster can be found at this hyperphysics website.

Today the remains of the reactor lie entombed in a concrete sarcophagus, a silent reminder of the Chernobyl nuclear accident.

The Eigenvalue Problem

An image of fiber tracts in the brain
using Diffusion Tensor Imaging.
From: Wikipedia.

In Intermediate Physics for Medicine and Biology, Russ Hobbie and I consider many mathematical topics. We analyze partial differential equations, Fourier transforms, vector calculus, probability, and special functions such as Bessel functions and the error function. One mathematical technique we never analyze is the central problem of linear algebra: the eigenvalue problem.

Calculating the eigenvalues and eigenvectors of a matrix has medical and biological applications. For example, in Chapter 18 of IPMB, Russ and I discuss diffusion tensor imaging. In this technique, magnetic resonance imaging is used to measure, in each voxel, the diffusion tensor, or matrix.

This matrix is symmetric, so D_xy = D_yx, etc. It contains information about how easily spins (primarily protons in water) diffuse throughout the tissue, and about the anisotropy of the diffusion: how the rate of diffusion changes with direction. White matter in the brain is made up of bundles of nerve axons, and spins can diffuse down the long axis of an axon much easier than in the direction perpendicular to it.

Suppose you measure the diffusion matrix to be

How do you get the fiber direction from this matrix? That is the eigenvalue and eigenvector problem. Stated mathematically, the fibers are in the direction of the eigenvector corresponding to the largest eigenvalue. In other words, you can determine a coordinate system in which the diffusion matrix becomes diagonal, and the direction corresponding to the largest of the diagonal elements of the matrix is the fiber direction.

The eigenvalue problem starts with the assumption that there are some vectors r = (x, y, z) that obey the equation Dr = Dr, where D in bold is the matrix (a tensor) and D in italics is one of the eigenvalues (a scalar). We can multiply the right side by the identity matrix (1’s along the diagonal, 0’s off the diagonal) and then move this term to the left side, and get the system of equations

One obvious solution is (x, y, z) = (0, 0, 0), the trivial solution. There is a beautiful theorem from linear algebra, which I will not prove, stating that there is a nontrivial solution for (x, y, z) if and only if the determinant of the matrix is zero

I am going to assume you know how to evaluate a determinant. From this determinant, you can obtain the equation

This is a cubic equation for D, which is in general difficult to solve. However, you can show that this equation is equivalent to

Therefore, the eigenvalues of this diffusion matrix are 4, 1, and 1 (1 is a repeated eigenvalue). The largest eigenvalue is D = 4.

To find the eigenvector associated with the eigenvalue D = 4, we solve

The solution is (1, 1, 1), which points in the direction of the fibers. If you do this calculation at every voxel, you generate a fiber map of the brain, leading to beautiful pictures such as you can see at the top of this post, and here or here.

Sometimes anisotropy can be a nuisance. Suppose you just want to determine the amount of diffusion in a tissue independent of direction. You can show (see Problem 49 of Chapter 18 in IPMB) that the trace of the diffusion matrix is independent of the coordinate system. The trace is the sum of the diagonal elements of the matrix. In our example, it is 2+2+2 = 6. In the coordinate system aligned with the fiber axis, the trace is just the sum of the eigenvalues, 4+1+1 = 6 (you have to count the repeated eigenvalue twice). The trace is the same.

Now you try. Here is a new homework problem for Section 13 in Chapter 18 of IPMB.

Problem 49 1/2. Suppose the diffusion tensor in one voxel is

a) Determine the fiber direction.

b) Show explicitly in this case that the trace is the same in the original matrix as in the matrix rotated so it is diagonal.

One word of warning. The examples in this blog post all happen to have simple integer eigenvalues. In general, that is not true and you need to use numerical methods to solve for the eigenvalues.

Have fun!

Darcy’s Law

Table 4.3 of Intermediate Physics for Medicine and Biology contains five transport equations. Each has the form “flux density equals a coefficient times the negative of a gradient of some quantity.” The table includes the flux of particles with the coefficient being the diffusion constant, the flux of heat with the coefficient being the thermal conductivity, the flux of momentum with the coefficient being the viscosity, and the flux of charge with the coefficient being the electrical conductivity. Are there other examples of transport equations important in biology and medicine? Yes. For instance, consider Darcy’s law.

Darcy’s law governs the flow of fluid through a porous medium. It is used to model the movement of groundwater through sedimentary rock, but it also describes the flow of water in tissue's extracellular space. Using a notation consistent with Table 4.3, we can write Darcy’s law as

j_v = - K dp/dx

where j_v is the flux density of fluid volume, p is the pressure, and K is the hydraulic conductivity. The units for j_v are m³ m^-2 s⁻¹, or m s⁻¹; therefore j_v corresponds to the speed of flow. Pressure has units of pascals, so dp/dx is expressed in Pa m⁻¹. Therefore, the units of hydraulic conductivity are m² Pa⁻¹ s⁻¹. Hydraulic conductivity is analogous to electrical conductivity or thermal conductivity; it specifies how well a material permits the transport of a quantity (flow of water) caused by some driving force (pressure gradient).

Russ Hobbie and I don’t discuss Darcy’s law in IPMB, but we come close. In Chapter 5 we analyze the flow of water across a membrane, and define the relationship

j_v = L_p Δp ,    (5.9)

where j_v again is the speed of flow, Δp is the pressure difference across the membrane, and L_p is the hydraulic permeability. If the membrane has a thickness Δx, then we can multiply and divide by Δx and obtain j_v = (L_p Δx) (Δp/Δx). The equation looks just like Darcy’s law (except for a minus sign), where the hydraulic conductivity is the hydraulic permeability times the membrane thickness:

K = L_p Δx.

I first encountered Darcy’s law when reading my friend Peter Basser’s paper about “Interstitial Volume, Pressure, and Flow During Infusion into the Brain” (Microvascular Research, 44:143–165, 1992). He derived a model of swelling in the brain that occurs during infusion of a drug. When Basser combined Darcy’s law with the equations of elasticity, he derived a diffusion equation for volume change of the tissue caused by accumulation of interstitial fluid (swelling), in which the diffusion constant is approximately the hydraulic conductivity times the bulk modulus.

Darcy’s law plays a key role in governing fluid flow in many tissues. A nice summary can be found in “Interstitial Flow and Its Effects in Solft Tissues” by Melody Swartz and Mark Fleury (Annual Review of Biomedical Engineering, 9:229–256, 2007). Below is the abstract to their review.

Interstitial flow plays important roles in the morphogenesis, function, and pathogenesis of tissues. To investigate these roles and exploit them for tissue engineering or to overcome barriers to drug delivery, a comprehensive consideration of the interstitial space and how it controls and affects such processes is critical. Here we attempt to review the many physical and mathematical correlations that describe fluid and mass transport in the tissue interstitium; the factors that control and affect them; and the importance of interstitial transport on cell biology, tissue morphogenesis, and tissue engineering. Finally, we end with some discussion of interstitial transport issues in drug delivery, cell mechanobiology, and cell homing toward draining lymphatics.

Strat-O-Matic Baseball

My Die-Hard Cub Fan Club
membership card.

Monday is opening day!

When I was young I was an avid baseball fan. I still enjoy the game, but now I haven’t time to follow it closely. My childhood team was the Chicago Cubs. I can still remember the lineup: shortstop Don Kessinger led off, second baseman Glenn Beckert hit next, left fielder Billy Williams batted third, and third baseman Ron Santo was cleanup. Ferguson Jenkins was the pitching ace, colorful Joe Pepitone—a former Yankee—arrived by trade to play first, Mr. Cub Ernie Banks was in the twilight of his career, and hot-tempered Leo Durochur was the manager. The Miracle Mets broke my heart in 1969, when the Cubs led their division into September only to collapse in the season's final weeks. The Cubs have not won the World Series since 1908, but I still love ’em. Maybe this year?

I wasn’t a good little league player; I struck out a lot, and I was assigned to play right field, where I could do the least damage with my glove. Yet, I had fun. One summer when I was in junior high, because of the timing of the age cutoffs and my birthday, I was nearly the oldest player in my age group. That was my best summer, when I approached mediocrity. I enjoyed the sport so much that I volunteered to manage the high school team. For those not familiar with baseball, being the manager in high school is very different than managing a professional team. In high school, the manager washes the uniforms, keeps track of the equipment, collects player statistics, and—my favorite job—draws the foul lines on the field before each game.

Strat-O-Matic Baseball.

When growing up in Morrison, Illinois, my friend Ted Paul owned the game Strat-O-Matic Baseball. It was played with dice and player cards, allowing you to recreate baseball games from your armchair. Unfortunately, Strat-O-Matic Baseball was expensive. We were not poor, but the price was out of the range my parents spent on birthday or Christmas presents. Necessity is the mother of invention, so I reverse engineered the game, making my own cards and rules that mimicked Strat-O-Matic’s in some ways but in other ways were my own creation.

Homemade Strat-O-Matic baseball cards
from the Oakland A’s, the dominant team
of that era (circa 1973).

In order to make my version of Strat-O-Matic Baseball, I had to learn the basics of probability. I didn’t need advanced concepts, and you can find all the necessary probability theory in Chapter 3 of Intermediate Physics for Medicine and Biology. Two ideas are key. First, the probability that one or the other of two mutually exclusive events happens is found by adding their individual probabilities. For instance, the probability of rolling either a one, two, or three on a single die is equal to the probability of rolling a one plus the probability of rolling a two plus the probability of rolling a three. Second, the probability that two independent events both happen is found by multiplying their individual probabilities. For example, the probability of throwing a one on the first die and a three on the second is equal to the probability of throwing a one times the probability of throwing a three. This concept underlies the joint probability distribution described in Appendix M of IPMB. These two rules, plus some counting, is all the math required to recreate Strat-O-Matic baseball. I also needed a source of baseball statistics, supplied by Street and Smith’s Baseball Yearbook, published each year around Valentine's Day and well within the family gift budget. In retrospect, making my own version of Strat-O-Matic Baseball was not difficult, but for a twelve-year-old kid I think I did a pretty good job.

Let me explain briefly how Strat-O-Matic Baseball works. The game was based on batters’ cards and pitchers’ cards. First you roll one die, and if you get a 1, 2, or 3 you use the batter’s card; a 4, 5, or 6 means you use the pitcher's card. Then you roll two dice which determine the outcome of the at-bat: out, walk, single, double, triple, or home run. The trick is to match the player’s statistics to the probability of a particular throw of the dice. The pitchers’ cards were hardest to create, because Street and Smith didn’t tabulate batting averages given up by pitchers, so I had to invent an algorithm based on wins, earned run average, and strikeouts. I remember spending many hours playing my homemade Strat-O-Matic baseball. In some ways it was pathetic: a child playing alone in his room with just his dice and cards. But in other ways it was romantic: thrilling late night ballgames with all the drama and excitement of sports, but performed just for me.

Even now, when I teach probability I focus on those key concepts I used when creating my version of Strat-O-Matic Baseball. Sometimes you learn more when you play than when you work.

Basic Physics of Nuclear Medicine

I’m cheap and I’m proud of it; I love free stuff. Intermediate Physics for Medicine and Biology isn’t free. Russ Hobbie and I appreciate our readers’ willingness to spend their money to purchase our book. Thank you! But what if you want more? What if—heaven forbid—you find our book is not totally clear, complete, or comprehensive? In IPMB we cite many references at the end of each chapter, so you have many sources of additional information. But often these sources cost money or may be difficult to obtain. Is there anywhere you can go online for free to augment IPMB?

A screenshot of the wikibook
Basic Physics of Nuclear Medicine.

One option is the wikibook Basic Physics of Nuclear Medicine. This book covers much of the same material as in the last half of IPMB. It analyzes in depth nuclear medicine (our Chapter 17), but it also covers the interaction of radiation with tissue (our Chapter 15), Fourier methods and tomography (our Chapters 11 and 12), detectors and x-ray imaging systems (our Chapter 16), ultrasound (our Chapter 13), and even a little magnetic resonance imaging (our Chapter 18).

Some of my favorite parts of the wikibook are not covered in IPMB:

• An analysis of using dual-energy radiography to remove the bones from an x-ray image.
• A chapter on computers in nuclear medicine.
• A discussion of the Picture Archiving and Communication System (PACS) and image processing.
• An overview of three dimensional visualization techniques.

What are the advantages of IPMB? For one thing, IPMB has a large collection of homework problems, more extensive than in Basic Physics of Nuclear Medicine. Also, I think our book has a better focus on using mathematical modeling to illustrate medical and biological physics concepts. Moreover, the entire first half of IPMB—about biomechanics, biothermodynamics, diffusion, bioelectricity, biomagnetism, and feedback—is absent from Basic Physics of Nuclear Medicine. Finally, and most importantly, Basic Physics of Nuclear Medicine doesn’t have a blog with weekly updates.

If you are looking for a free, easily accessible online textbook to use as a supplement (please, not a replacement!) for Intermediate Physics for Medicine and Biology, consider Basic Physics of Nuclear Medicine. It’s worth every penny.